To calculate the reaction rate of the S![]() 2 reaction
in aqueous solution, it is not correct to take the computed free energy
difference (
2 reaction
in aqueous solution, it is not correct to take the computed free energy
difference (
![]() kcal/mol) and plug it into the textbook
relations
kcal/mol) and plug it into the textbook
relations
for two reasons.
In the first place, is the exponential term,
![]() related to the Boltzmann probability
related to the Boltzmann probability
![]() to find the reacting system in the transition state independent of the exact
starting configuration in the reactant well. Thus, instead of taking
to find the reacting system in the transition state independent of the exact
starting configuration in the reactant well. Thus, instead of taking
![]() , the Boltzmann factor is obtained
by integration over the reactant well of the free energy profile, using
, the Boltzmann factor is obtained
by integration over the reactant well of the free energy profile, using
As the energy will increase rapidly as ![]() decreases below zero
(since it is associated with configurations in which none of the Cl's are
chemically connected to the CH
decreases below zero
(since it is associated with configurations in which none of the Cl's are
chemically connected to the CH![]() part), it is not necessary to calculate
the profile
part), it is not necessary to calculate
the profile ![]() up to
up to
![]() . Also, we note that the
profile is dependent on the size of the periodic supercell, simply because
the available space, and therefore the entropy, of the system at a certain reactant
state constraint value (say
. Also, we note that the
profile is dependent on the size of the periodic supercell, simply because
the available space, and therefore the entropy, of the system at a certain reactant
state constraint value (say ![]() ) increases with the box size. (Obviously,
the probability to find the two reactants in the transition state is much smaller
in an ocean of liquid than in a small box with a few tens of water molecules).
Normalizing the Boltzmann factor with the concentration gives the correct result
for the transition state theory rate for the second order rate coefficient.
) increases with the box size. (Obviously,
the probability to find the two reactants in the transition state is much smaller
in an ocean of liquid than in a small box with a few tens of water molecules).
Normalizing the Boltzmann factor with the concentration gives the correct result
for the transition state theory rate for the second order rate coefficient.
In the second place, does the free energy in the exponential term of
equation 3.9 include a correction for the fact that not in all
occasions that the system reaches the transition state, it actually crosses
the barrier to end up in the product well. Instead, the computed Boltzmann
factor (equation 3.10) is an ensemble average that only
gives the (transition state theory) upper limit of the rate constant ![]() ,
assuming that every time the barrier top is reached, the products are subsequently
formed. Multiplying
,
assuming that every time the barrier top is reached, the products are subsequently
formed. Multiplying ![]() by the so-called transmission coefficient,
by the so-called transmission coefficient,
![]() , gives the true rate constant. The transmission coefficient is a
time dependent function, which correlates the initial velocity of the system along the
reaction coordinate,
, gives the true rate constant. The transmission coefficient is a
time dependent function, which correlates the initial velocity of the system along the
reaction coordinate, ![]() , on top of the barrier at time
, on top of the barrier at time ![]() with
with ![]() at time
at time
![]() :
:
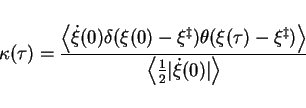 |
(57) |
For a reaction in solution ![]() is related to the coupling
is related to the coupling ![]() between the reactants and the solvent, as schematically drawn in
figure 3.7. At low reactant-solvent coupling values
(aka Lindemann-Hinshelwood regime or energy diffusion regime), the energy
obtained by the reactants
from the solvent to reach the barrier top cannot be dumped rapidly back to
the solvent environment after crossing the barrier. As a result, the reactant
complex retains enough energy to cross the transition barrier back and forth
until it finally loses the energy and the correlation between
between the reactants and the solvent, as schematically drawn in
figure 3.7. At low reactant-solvent coupling values
(aka Lindemann-Hinshelwood regime or energy diffusion regime), the energy
obtained by the reactants
from the solvent to reach the barrier top cannot be dumped rapidly back to
the solvent environment after crossing the barrier. As a result, the reactant
complex retains enough energy to cross the transition barrier back and forth
until it finally loses the energy and the correlation between ![]() and the final value of
and the final value of ![]() is low, hence a small transmission coefficient
is low, hence a small transmission coefficient
![]() which is proportional to
which is proportional to ![]() .
At the other side (aka Kramers regime or spatial diffusion regime), the reactant
complex is pushed back and forward by the fluctuation in the solvent environment,
which also results in a small correlation and thus a small
.
At the other side (aka Kramers regime or spatial diffusion regime), the reactant
complex is pushed back and forward by the fluctuation in the solvent environment,
which also results in a small correlation and thus a small ![]() which is inversely
proportional to
which is inversely
proportional to ![]() . In between
these two reactant-solvent coupling extremes
. In between
these two reactant-solvent coupling extremes ![]() has values closer to
unity.
has values closer to
unity.
For the S![]() 2 reaction in water, we see that a large force
pulls the [Cl
2 reaction in water, we see that a large force
pulls the [Cl![]() CH
CH![]() Cl]
Cl]![]() complex along the reaction coordinate
in the either direction if the solvation of the two chloride groups becomes
unbalanced (compare table 3.7 and figure 3.5). In order
for the system to proceed to either side, one Cl has to gain solvent molecules
in the solvation shell, whereas the other Cl has to expel H
complex along the reaction coordinate
in the either direction if the solvation of the two chloride groups becomes
unbalanced (compare table 3.7 and figure 3.5). In order
for the system to proceed to either side, one Cl has to gain solvent molecules
in the solvation shell, whereas the other Cl has to expel H![]() O molecules.
Due to this very strong coupling between the solvent environment and the
reaction complex, a low transmission coefficient is expected for the S
O molecules.
Due to this very strong coupling between the solvent environment and the
reaction complex, a low transmission coefficient is expected for the S![]() 2
reaction in water.
2
reaction in water.