Appendix A: Force of constraint

The system can be constrained to a hyperplane $\xi({\bf r})=\xi^\prime$ in phase space in a molecular simulation, by extending the Lagrangian with a term $\lambda \cdot (\xi({\bf r})-\xi^\prime)$, with ${\bf r}$ the atomic positions, $\xi$ our reaction coordinate, and $\lambda$ the Lagrange multiplier associated with the force on the holonomic constraint. Each atom $i$ then feels a constraint force, equal to $F_i(\xi)=\lambda (d\xi/dr_i)$. It is well known that the use of constraints affects the phase space distribution (see e.g. ref frenkel_smit). For a velocity-independent property $p$, the bias introduced by a constraint can be compensated using the relation

$$\langle p({\bf r})\rangle^{\mathrm{unconstr.}} = \frac{\la... ...-1/2} p({\bf r}) \rangle_{\xi}}{\langle Z^{-1/2}\rangle_{\xi}}$$ (51)

where the factor $Z$ is defined by

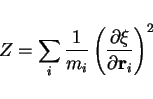$$Z = \sum_{i} \frac{1}{m_i} \left( \frac{\partial\xi}{\partial {\bf r}_i} \right)^2$$ (52)

This was generalized recently for velocity dependent properties, such as the the mean force of constraint[17,76]. In the formulation of reference otterw3 it reads:

$$F(\xi) = \frac{\langle\lambda_\xi Z^{-1/2}\rangle_{\xi} + \... ...xi \cdot \nabla_i Z \rangle_\xi}{\langle Z^{-1/2}\rangle_\xi}$$ (53)

where $T$ is the temperature, $k_B$ is Boltzmann's constant, and $m_{i}$ is the mass of particle $i$.

The second term in the numerator of equation 3.7 arises because the mean force of constraint depends on the velocities, through the kinetic term $\partial K/ \partial \xi$ in the force of constraint (equation 1). In their work, they demonstrated the importance of the corrections for a constrained bending angle of a tri-atomic molecule and for a constrained dihedral angle in a tetra atomic molecule.

In table 3.8, we show the results for the mean force of constraint for our S$_\mathrm{N}$2 reaction using the constraint of equation 2, once as $\lambda$, once corrected according to equation 3.5 and once using equation 3.7. As the differences are very small, the bias on our system introduced by the constraint must by very small.

Table 3.8: The average constraint force for the different reaction coordinate values $\xi$. The constraint force is shown once as the Lagrange parameter $\lambda$, once corrected according to equation 3.5 and once more with the full correction according to equation 3.7.

$\xi$	$\lambda$	$\langle Z^{-1/2}\cdot\lambda\rangle_{\xi}/\langle Z^{-\frac{1}{2}}\rangle_{\xi}$	$F(\xi)$
0.27	-0.0091	-0.0098	-0.0095
0.32	-0.0494	-0.0498	-0.0496
0.35	-0.0815	-0.0831	-0.0830
0.40	-0.2384	-0.2396	-0.2394
0.43	-0.3268	-0.3277	-0.3276
0.45	-0.2929	-0.2931	-0.2930
0.50	-0.0408	-0.0408	-0.0408
0.55	0.2570	0.2572	0.2571
0.60	0.1955	0.1966	0.1964
0.70	0.0018	0.0004	0.0002