S$_\mathrm{N}$2 reaction in water

Figure 3.5: The mean force of constraint $\left <F \right >_{\xi }$ (dashed line; right-hand-side axis) and the Helmholtz free energy $\Delta A$ (solid line; left-hand-side axis) versus the reaction coordinate $\xi$. The crosses denote the values from subsequent constrained MD runs, starting with a reaction coordinate value of $\xi =0.270$. The circles are from subsequent runs in the backward reaction coordinate direction, starting from the finished run with $\xi =0.55$. The three asterisks denote the points at $\xi =\{0.30, 0.40, 0.45\}$ mirrored in ($\xi$=0.5,$F$=0) to indicate the hysteresis. See also text.

In this section, we will discuss the results of the constrained molecular dynamics simulations performed to study the CH$_3$Cl + Cl$^-$ reaction in a dilute aqueous solution of HCl. To obtain the free energy barrier $\Delta A$, we calculated the mean force of constraint $\left< \partial H/\partial \xi\right>_{\xi}$ at 5 points ( $\xi = \{0.32, 0.35, 0.40, 0.45, 0.50\}$) along the reaction coordinate $\xi$ (Eqn. 2). As a verification of the simulations, $\left< \partial H/\partial \xi\right>_{\xi}$ was also calculated at three points at the product side of the reaction coordinate ( $\xi = \left\{0.55, 0.60, 0.70\right\}$). Subsequently, two extra simulations were performed for the points $\xi = 0.27$ (because at $\xi =0.32$ there was still too large an attraction between CH$_3$Cl and Cl$^-$, whereas for the separated reactants, the interaction between the reactants is expected approach to zero and at $\xi = 0.43$ (where we expected an extremum in $\left< \partial H/\partial \xi\right>_{\xi}$, after having fitted the first five points).

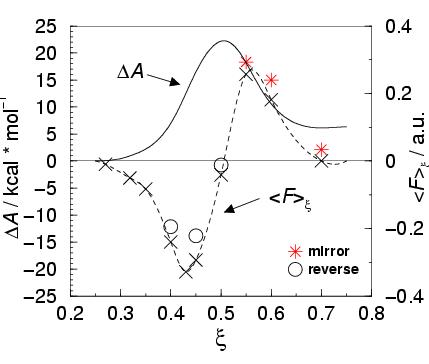
The results for the mean force of constraint are plotted in figure 3.5 (and listed in table 3.8). The dashed line is a cubic spline fitted to the calculated points. Integration of the mean force of constraint with respect to $\xi$ (according to equation 3.7) results in the free energy barrier, shown by the solid line in the figure, yielding a barrier height of 22.2 kcal/mol. Taking into account the 8 kcal/mol error in the gas phase reaction, the free energy barrier of the reaction in aqueous solution would be 30.2 kcal/mol; an overestimation of about 3.6 kcal/mol compared to the experimental result of 26.6 kcal/mol [66].

Because of the symmetry of the reaction the calculated energy profile should be symmetric. From the figure, it is obvious that the shape has a significant asymmetry. This asymmetry has been illustrated by asterisks in the figure. They have been drawn in figure 3.5 above the three points at the product side of the reaction ( $\xi=\{0.55, 0.60, 0.70\}$) to picture the equivalent points at the reactant side (with the negative force) for comparison. Moreover, the mean force of constraint does not vanish at the transition state $\xi =0.5$ as it should. The three product-side points as well as the point at the transition state apply to $\left[\mathrm{Cl}\cdots \mathrm{CH}_3 \cdots \mathrm{Cl} \right]^-$ configurations with a driving force that is smaller toward the product-side (or larger toward the reactant-side) than was expected from the other points at the reactant-side. This can be characterized as hysteresis when forcing the reaction by the method of constraint. Most likely, this hysteresis is due to the surrounding water shell, which apparently adapts too slowly to the changing reactants configuration, when going from one simulation to the next by increasing $\xi$.

To test this explanation, we performed calculations for the reversing of the reaction. We performed the backward reaction for three points ( $\xi=\{0.50, 0.45, 0.40\}$), where we started from the constrained MD run at $\xi =0.55$ and moved the constraint value slowly to the previous point on the reaction coordinate. Subsequently, we equilibrated for 2.5 ps, collected the force of constraint for 3 ps, and moved on to the next point, similar to the points of the forward reaction direction. The results are shown by the circles in figure 3.5. The hysteresis at the first point, $\xi=0.50$, has disappeared since $\left<F (0.5)\right>_{\xi}$ is zero (within the error in the force), as expected. Apparently, the solvent configuration is not pulling on either side of the reacting complex, at this point. For the other two points, we now find smaller absolute values for the mean force of constraint than we found in the forward reaction. This is consistent with the picture of a ``memory effect'' in the solvent, i.e. a too slow adaptation of the water configuration to the changed reaction coordinate.

A rough estimate of the systematic error on the free energy barrier due to the hysteresis can be made, by assuming that the deviation in the force will increase linearly from zero at the starting point of the separate reactants ( $\xi \approx 0.25$) to the observed -0.041 a.u. at the transition state. Correcting the free energy profile for the corresponding overestimation (3.2 kcal/mol), gives a barrier height of 27 kcal/mol. The excellent agreement with experiment (26.6 kcal/mol), after the corrections for the DFT-GGA error in the gas phase transition state energy and the hysteresis in the constrained MD runs, must be a bit fortuitous, for the following reasons. First of all we have found the accuracy of the DFT-BP description of the energetics of the solvation to be of the order of 1 kcal/mol. Secondly, the experimental result refers to more dilute solution at neutral pH, with typically potassium used for the counter cation. In the present calculation, a proton acted as counter-cation, which can be expected to have some influence on the energetics of the reaction via its charge and solvation structure.

Table 3.7: The coordination numbers of the water solvation shells around the attacking Cl$^\prime$ and the leaving Cl, at different points on the reaction coordinate. The coordination numbers were calculated by integration over the peak in the radial distribution function (a hyphen indicates there was no such peak). Numbers between parentheses indicate that the peak was too broad for an accurate estimate.

	Attacking chloride		Leaving chloride
$\xi$	$cn_{\mathrm{Cl^{\prime}-H}}$	$cn_{\mathrm{Cl^{\prime}-O}}$	$cn_{\mathrm{Cl-H}}$	$cn_{\mathrm{Cl-O}}$
0.27	5.4	6.3	-	-
0.32	4.3	5.1	-	-
0.35	4.9	4.6	-	-
0.40	4.7	4.4	-	-
0.43	4.8	4.8	-	-
0.45	4.2	4.5	1.1	4.4
0.50	3.3	4.3	2.7	(4.8)
0.50$^*$	2.9	(5.6)	3.0	(4.3)
0.55	2.2	(4.8)	4.0	5.0
$^*$ Coming back from $\xi =0.55$, see text.

Next, we turn to the structural aspects of the reaction. In figure 3.6, we compare the radial distribution functions of the water atoms with respect to the leaving and attacking chloride ions, calculated for the transition state and for the more separated reactants ($\xi =0.32$). From integration over the first peak of the distribution functions, the coordination numbers for the chloride ions were calculated and compiled in table 3.7 (for all simulated values of $\xi$).

Figure 3.6: Radial distribution of water around the leaving Cl atom (upper graphs) and attacking Cl$^\prime$ atom (lower graphs) for two points on the reaction coordinate, namely $\xi =0.5$ (the transition state: solid lines) and $\xi =0.32$ (initial reactants: dashed lines). The graphs on the left-hand-side show the distribution of the water oxygens, and the right-hand-side graphs the distribution of the water hydrogens. For comparison, dotted lines are drawn in for the $g_{\mathrm{Cl-O}}$ and $g_{\mathrm{Cl-H}}$ of CH$_3$Cl in water (upper graphs) and HCl in water (lower graphs).

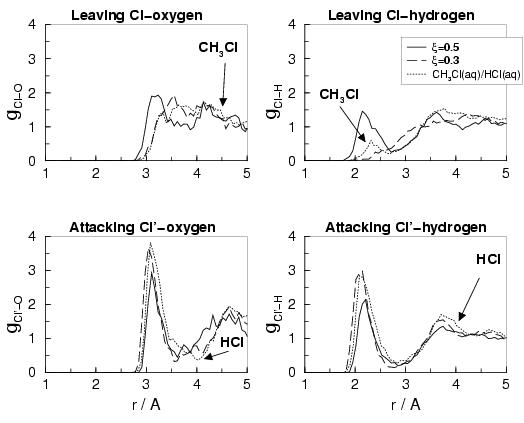
To start with the separated reactants at $\xi =0.32$, we note that the distribution functions $g_{\mathrm{Cl^\prime-O}}$ and $g_{\mathrm{Cl^\prime-H}}$ of the attacking chloride anion (dashed lines in the lower graphs) are very similar to the functions of pure HCl in water (dotted lines; see also figure 3.3). The distribution around the leaving chloride atom at $\xi =0.32$ (upper two graphs) is in agreement with pure CH$_3$Cl in water (dotted lines), except for a small peak in $g_{\mathrm{Cl-H}}$ at $r=2.3$ Å in the latter. The small peak in the pure CH$_3$Cl solution (case b) in section 3.2.4) can be attributed to one water molecule which is hydrogen bonded to the Cl of methylchloride. The main reason for the absence of this peak in $g_{\mathrm{Cl-H}}$ of the leaving Cl, must be the presence of the Cl$^-$ anion, which has a strong influence on the solvent structure. The coordination numbers (in table 3.7) shows that the attacking chloride anion is solvated by about five water molecules, whereas the separate CH$_3$Cl does not show any attraction of water atoms. Note that $cn_{\mathrm{Cl^{\prime}-H}}(\xi=0.32)=4.3$ confirms that this starting constrained simulation indeed does not fully resemble separated reactants as concluded in section 3.3.4, whereas the extra simulation of $\xi = 0.27$ shows coordination numbers of 5.4 and 6.3 in agreement with the values for the pure HCl in water (5.2 and 6.5, table 3.5).

Next, we discuss the radial distribution functions for the transition state configurations (solid lines). These show a more equal solvation of the attacking and leaving chloride ions. However, the first peaks of the attacking chloride ion are still much more pronounced than the peaks arising from the first solvation shell around the leaving chloride. Also, the minimum at $r=3.5$ Å is much deeper in $g_{\mathrm{Cl^{\prime}-O}}$ than in $g_{\mathrm{Cl-O}}$. This asymmetry in the chloride solvation is reflected less strongly in the coordination numbers (table 3.7). The attacking chloride still has on average 3.3 hydrogens in the first shell, while the leaving chloride has only 2.7. The Cl-O coordination numbers cannot be determined accurately because the oxygen distribution function $g_{\mathrm{Cl-O}}$ of the leaving Cl does not show an unambiguous minimum. Still, from the hydrogen distribution, we can conclude that the attacking Cl is stronger solvated than the leaving Cl, at $\xi =0.5$, which must be the grounds for the effective force of constraint at the transition state. Indeed, in the reversed reaction direction, where we found the expected $\left<F (0.5)\right>_{\xi}=0$, we also see a more symmetric hydrogen distribution (radial distribution functions not shown) and coordination number: 2.9 for the attacking Cl and 3.0 for the leaving Cl. Just before the transition state, the leaving chloride has only one hydrogen in the ``first shell'' ( $cn_{\mathrm{Cl-H}}(\xi=0.45)=1.1$), whereas just after the transition state the attacking chloride still has two hydrogens ( $cn_{\mathrm{Cl^{\prime}-H}}(\xi=0.55)=2.2$). This difference leads to a larger value for the mean force of constraint at $\xi=0.45$ in comparison with $\xi =0.55$, and gives a structural explanation for the observed hysteresis in the free energy profile of figure 3.5.