S$_\mathrm{N}$2 reaction in gas phase

To study the solvation effects on the reaction between CH$_3$Cl with Cl$^-$, we will first consider the gas phase reaction. Starting with separated reactants, the reaction energy $\Delta E(\xi)$ decreases as the attacking chloride anion approaches the dipolar CH$_3$Cl from the carbon side to form a reaction complex, with complexation energy $\Delta E^{\mathrm{RC}}$ (see figure 3.4). Moving along to the product side, $\Delta E(\xi)$ increases until the reactants arrive at the $D_{3h}$ symmetric transition state, with energy $\Delta E^{\mathrm{TS}}$. The product side of the profile is symmetric to the reactant side. The numerous attempts to estimate $\Delta E^{\mathrm{RC}}$ and $\Delta E^{\mathrm{TS}}$ have resulted, especially for the latter, in a variety of values for these quantities. A selection of these energies and the corresponding geometries found in the literature, as well as our own results are compiled in table 3.6. For the ion-dipole reaction complex energy, the best ab initio number is probably given by the G2 calculation of Glukhovtsev et al.: $\Delta E^{\mathrm{RC}}= -10.5$ kcal/mol.[58,123] Our DFT results and the ab initio and DFT results from literature are all within 1 kcal/mol to this number. Also the experimental estimate by Larson and McMahon agrees within their error estimate with this value. Only the CISD (configurational interaction, including single and double excitations) result by Vetter and Zülicke is about 2 kcal/mol too low.

Table 3.6: Bonding energy and geometry of the reaction complex (RC) and the transition state (TS) in gas phase at $T=0$ K compared to other methods

	Reaction complex			Transition state
	$\Delta E^{\mathrm{RC}}$	$R_{\mathrm{CCl}}$	$R_{\mathrm{CCl^\prime}}$	$\Delta E^{\mathrm{TS}}$	$R_{\mathrm{CCl}}$	$\Delta E^{\mathrm{barrier}}$
	[kcal/mol]	[Å]	[Å]	[kcal/mol]	[Å]	[kcal/mol]
CP-PAW/BP	-10.39	1.91	3.01	-5.32	2.37	5.1
ADF-BP	-10.96	1.88	3.09	-5.30	2.35	5.7
DFT-BP$^a$	-10.3	1.835	3.098	-5.7	2.342	4.6
MP2$^a$	-10.5	1.808	3.266	3.5	2.316	14.0
MP4$^a$	-10.6			1.8		12.4
MP2$^b$				4.01	2.28
CCSD(T)$^b$				2.65	2.301
G2$^c$	-10.51	1.810	3.270	2.76	2.317	13.26
DFT-B3LYP$^d$	-9.72	1.858	3.180	1.1	2.371	10.8
HF/CISD$^e$	-8.7	1.823	3.384	8.7	2.408	17.5
MP2$^f$	-9.66	1.808	3.267	7.68	2.316	17.34
B3LYP$^f$	-9.52			-0.85		8.67
Expt.	-8.6 $\pm$ 0.2$^g$			1. $\pm$ 1.$^h$		13.2 $\pm$ 2.2$^h$
	-12.2 $\pm$ 2$^i$

$^a$ Ref debrzi94 Deng and Ziegler 1994 6-31G(d,p). $^b$ Ref bot98 Coupled cluster calculations by Peter Botschwina. $^c$ Ref GlPrRa95 Glukhovtsev, Pross and Radom, at $T=300$ K, G2 method effectively QCISD(T)/6-311+G(3df,2p) + ZPE correction for energies and MP2/6-311+G(3df,2p) for geometries. $^d$ Ref GlPrRa96 Glukhovtsev, Bach, Pross and Radom, basis set: 6-311+G(3df,2p). $^e$ Ref VeZu90 Vetter and Zülicke, geometries using Hartree Fock and energies using all electron CISD with Davidson correction and DZDP basis set quality. $^f$ Ref StChAb97 Streitwieser 1997, basis set: 6-31G*. $^g$ Ref DoDaRo73 Dougherty et al. high pressure mass spectrometry. $^h$ Ref BaDoBi88 From measurement of the rate coefficient at temperatures above $T=300$ K using a flowing afterglow technique and a simplified modification of RRKM theory. $^i$ Ref LaMc85 Larson and McMahon, using ion cyclotron resonance.

Figure 3.4: The energy profile for the gas phase reaction calculated with ADF (triangles and solid line) and CP-PAW (crosses and dotted line). The zero-point energy and temperature contributions to the internal energy are very small at $T=300$ K ( $\Delta H_{\mathrm{300K}}$, circles and dashed line). Due to the much lower entropy of the reactant complex and transition state compared to the free reactants, the Gibbs free energy barrier $\Delta G = \Delta H - T\Delta S$ is much higher than the internal energy barrier (squares and solid line).

The results for the transition state energies, varying from -5.7 till 8.7 kcal/mol (see table 3.6) have lead to a number of conflicting views. For instance, Streitwieser et al. (ref StChAb97) concluded: ``the large differences in TS properties between MP2 and B3LYP suggest that the latter may not always be reliable for TS structures''. And Deng et al. (ref debrzi94) concluded that ``the experimental data (for $\Delta E^{{\mathrm TS}}$ and $\Delta E^{{\mathrm{barrier}}}$) seem to fall in the region with the MP4 and NL-SCF (= DFT-BP) value as the upper and lower bounds, respectively.'' The highest-level ab initio result for $\Delta E^{{\mathrm TS}}$ is the CCSD(T) calculation by Botschwina, equal to 2.65 kcal/mol. The G2 estimate by Glukhovtsev et al. agrees very well with it, as well as the approximate experimental result of 1.0 $\pm$ 1.0 kcal/mol. This would imply that the DFT-BP result of -5.7 kcal/mol by Deng is just too low, and underestimates $\Delta E^{{\mathrm TS}}$ significantly. Streitwiesers MP2 result of 7.7 kcal/mol seems erroneous, compared to the MP2 results of Botschwina (4.01 kcal/mol) and Deng et al. (3.5 kcal/mol). The overestimation of the CISD energy (8.7 kcal/mol) is probably due to a combination of an inaccurate (HF) geometry and a too small basis set (DZDP).

There are indications that the too low transition state energy by DFT-BP is systematic for structures with a symmetrical three-center four-electron bond, such as the $\sigma$-bond in Cl-C-Cl. For example, Gritsenko et al.[124] investigated the very similar $[\mathrm{F-CH}_3\mathrm{-F}]^-$ transition state structure. They concluded that the delocalization of the exchange hole over the three atoms in combination with a very small non-dynamical correlation, is erroneously represented by the exchange part of the GGA density functional, which introduces a localized hole and thus a spurious non-dynamical correlation[124]. This is, of course, important to keep in mind as we proceed to the S$_\mathrm{N}$2 reaction in water solution. Anticipating the results for the reaction in aqueous solution, we may expect that the transition state in the solvated case is underestimated by an amount in the order of 8 kcal/mol because of the similarity in the geometric and electronic structure of the reacting species. The accuracy of the solvation effects should, in principle, be in the order of 1 kcal/mol, as followed from the simulations in the previous sections.

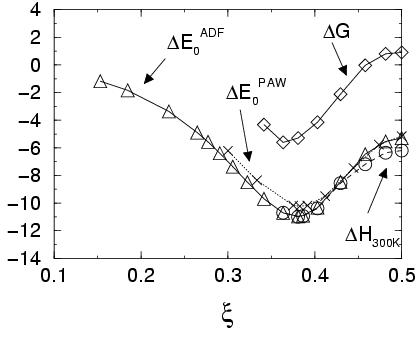
Figure 3.4 plots the reaction energy profile, as well as the reaction enthalpy $\Delta H$ and the free energy $\Delta G$. The latter two are calculated only between the reactant complex and the transition state because of the failure of the smooth change of vibrational contributions into translational and volume work contributions for further separated reactants. The total correction to the calculated energy $\Delta E_0$ to obtain the enthalpy $\Delta H$ at a temperature of $T=300$ K (see eqn 3.3) is very small for the ion-dipole complex. It amounts to less than 0.1 kcal/mol for the equilibrium geometry, and -0.9 kcal/mol for the transition state. This is in good agreement with the estimates by Vetter and Zülicke (0.1 kcal/mol and -0.5 kcal/mol, respectively). The formation of the ion-dipole complex from infinitely separated reactants involves a large negative entropy change, equal to $T \Delta S = -5.5$ kcal/mol. The entropy difference ($T \Delta S$) of the transition state with respect to the free reactants is -7.1 kcal/mol, which means that the intrinsic free energy reaction barrier is about 1.6 kcal/mol higher than the internal energy barrier.