Water and hydrochloric acid

The last two test cases, before actually treating the S$_\mathrm{N}$2 reaction, deal with CP-PAW molecular dynamics simulations of water and hydrochloric acid (HCl) in water (i.e. cases (a) and (d) in section 3.2.4. The pure water sample consisted of 32 water molecules in a periodic cubic box with an edge of 9.8650 Å, which was taken from a previous empirical force-field MD simulation. After equilibrating for 15 ps to obtain natural distributions for the atomic positions and velocities at $T=300$ K, we computed a trajectory of 8.6 ps, from which some structure and dynamics parameters for liquid water were calculated. The hydrochloric acid sample was obtained from the equilibrated water sample by inserting one HCl molecule and scaling the cubic box up to an edge of 9.9684 Å to yield the experimental density of a 1:32 ratio of HCl to H$_2$O molecules (1.66M) solution. The equilibration time for the HCl and 32 water molecules system was 10 ps and the following 7.7 ps of trajectory was again used for analysis.

Figure: Radial distribution of water at $T=300$ K (solid lines) compared to the Car-Parrinello simulation from ref SHP (dashed lines) and the neutron diffraction data from ref Soper (dotted lines).

The calculated radial distribution functions of the pure water sample are shown in figure 3.2. As expected, our results obtained using the CP-PAW method are very similar to the CP-MD results by Sprik, Hutter and Parrinello[51], with a small discrepancy in the depth after the first peak in $g_{\mathrm{OO}}$. When compared to neutron diffraction data, the peak values are overestimated and their positions shifted to smaller radii. The overall resemblance of the radial distribution is satisfactory, where we note that DFT-BP has a tendency to enhance structure of the liquid, as concluded earlier in ref SHP. The peak positions and coordination numbers are listed in table 3.4. In view of the experimental numbers quoted for the coordination numbers, this seems to be a quantity that is difficult to measure. Nevertheless, it can be seen from the table that the CP-PAW simulation underestimates the H$_2$O coordination somewhat. Comparing the CP-PAW calculations to MD results obtained using the TIP4P or SSD force fields shows similar values for the O-O peak position. However, force field results for the O-H peak position and the coordination numbers are larger than the CP-PAW results.

Table 3.4: Some properties of liquid water compared. Peak maxima $R_{\rm OH}$ and $R_{\rm OO}$ are given in Å. The coordination numbers $cn_{\rm OH}$ and $cn_{\rm OO}$ were estimated for all methods by integration of the first peak of $g_{\mathrm{OH}}$ and $g_{\mathrm{OO}}$ up to the next minimum (at resp. 2.3/3.25 Å for the AIMD results and 2.5/3.5 Å for the other methods). The experimental self diffusion coefficient $D=2.35\cdot 10^{-5}$ cm$^2$/s [107].

	$R_{\rm OH}$	$cn_{\rm OH}$	$R_{\rm OO}$	$cn_{\rm OO}$	$D$
CP-PAW	1.73	1.78	2.72	4.10	1.3 $\pm$ 0.7
SHP$^a$			2.72	3.9 $\pm$ 0.2	0.35 $\pm$ 30%
MC/MD(TIP4p)	1.9$^b$	1.9$^b$	2.75$^c$	5.1$^b$	3.3 $\pm$ 0.5$^d$
MD(SSD)$^e$	1.9	2.0	2.75	5.2	2.24 $\pm$ 2%
neutr. diff.$^f$	1.9	1.6-1.9	2.86	5.3
X-ray$^g$			2.7-2.8	4.3

$^a$ Ref SHP using Car-Parrinello MD simulations. $R_{\rm OO}$ was read from the graph. $^b$ From figure 1 in ref JoChMaImKl. $^c$ MD/TIP4 (transferable intermolecular potential-4 points) results from ref SpMaBe98. $^d$ MD/TIP4 results from ref WaKl89. $^e$ MD/SSD (soft sticky dipole model) results from ref LiIc96 and ChIc99. $^f$ Ref Soper using neutron diffraction. $^g$ Ref NaLe67 and ref NaLe71 using X-ray diffraction.

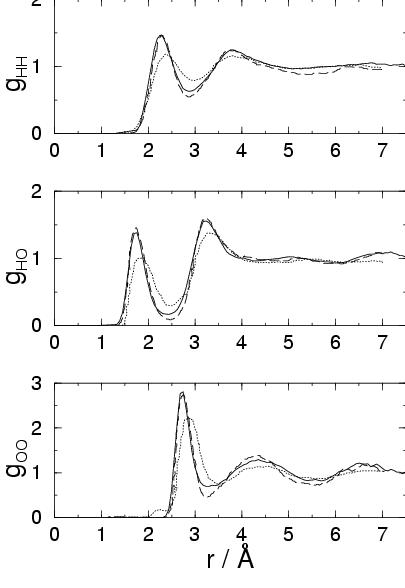
The self-diffusion coefficient $D$ in the pure water sample was calculated from the mean-square displacement. Due to the short simulated trajectory of 8.6 ps, the statistical error, estimated from 1 ps block averages, is relatively very high. Our result of $D=1.3\pm0.7\cdot10^{-5}$ cm$^2$/s lies between the experimental value[115] of $D^{\rm {exp}}=2.35\cdot10^{-5}$ cm$^2$/s and the value of $D^{\rm {AIMD}}=0.35\pm0.1\cdot10^{-5}$ cm$^2$/s from the CP-MD simulation of ref SHP.

Figure: Radial distribution around Cl$^-$ at $T=300$ K (solid lines) compared to the MD results using a polarizable semi-empirical force field from ref SpKlWa (dotted lines).

The results of the AIMD simulation of the dilute aqueous HCl solution are summarized in figure 3.3 and table 3.5 that show the Cl-H and Cl-O radial distribution functions and list the distribution peak positions and estimated coordination numbers, respectively.

AIMD simulations of aqueous HCl solutions have been reported earlier by Laasonen and Klein [117,118]. They considered systems of similar size (32 molecules) at various concentrations, the most dilute one (mole ratio 1:31) comparable to ours. However, they focused on the dissociation and the effect of concentration and reported only little on structural properties. As far as comparison was possible, their results agree within the statistical error margins with our findings. Aqueous HCl solutions have also been studied by molecular simulation using (semi-)empirical force fields. Here we can distinguish between simple non-polarizable[119] and more advanced polarizable[116] water models. Note that the force-field studies considered solvation of a single Cl$^-$, leaving out the H$^+$ counter-ion. A comparison with our results is therefore only possible to a limited extent.

Table 3.5: Structural parameters of Cl$^-$ in water compared with other molecular simulation results and experiment.

	$R_{\mathrm{Cl^--H}}$	$cn_{\mathrm{Cl^--H}}$	$R_{\mathrm{Cl^--O}}$	$cn_{\mathrm{Cl^--O}}$
CP-PAW	2.11	5.2	3.09	6.5(7.2)$^*$
MC/TIP4p$^a$	2.25	7.0	3.21	7.4
MD/TIP4p$^b$	2.34	7.0	3.27	7.2
MD/pol.$^c$	2.25	5.9	3.18	6.1
neutr. diff.$^d$	2.22-2.26	-	3.20-3.34	5.3-6.2
X-ray$^e$	-	-	3.10-3.35	5-11

$^a$ Ref ChSpJo using Monte Carlo simulations with the TIP4p potential. $^b$ Ref SpKlWa using Molecular Dynamics simulations with the TIP4p potential. $^c$ Ref SpKlWa using Molecular Dynamics simulations with a polarizable model. $^d$ Ref NeNeEn80 using neutron diffraction. $^e$ Ref EnNe81 using X-ray diffraction. $^*$ Peak integrated up to: $r=3.75$ Å as in literature, and in parenthesis: till the $g(r)$ minimum at $r=4.0$ Å.

From figure 3.3 and table 3.5 we see that peak positions obtained with our AIMD simulations are shifted somewhat to smaller radii compared those of the experiment and to the polarizable force-field MD simulation. Note also some enhanced structure of the second solvation shell, visible in the $g_{\mathrm{Cl-O}}$ distribution function beyond $r=4$ Å and also in $g_{\mathrm{Cl-O}}$ beyond $r=3.5$ Å. This structure is not present in the classical MD simulation. The observed differences need not be entirely due to the use of an ab initio (DFT) potential instead of an effective pair potential. It could also be attributed to the presence of the H$^+$ counter ion that resides on average in the second solvation shell. A second factor could be the small size of the periodic simulation box contributing to some extra structuring.

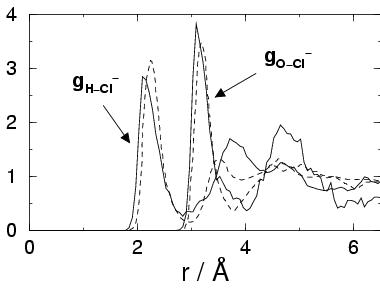
The coordination numbers listed in table 3.5 show that in our AIMD simulation Cl$^-$ has on average 5 hydrogen bonds, in good agreement with the findings of the CP-MD simulation of ref LaKl97 and the simulation with the advanced polarizable force field. Note that the non-polarizable force field overestimates the coordination of the hydrogens significantly. The oxygen coordination number from our AIMD simulation of 7.2 exceeds the results of the polarizable force field simulation by 1.1. Also the comparison with the experimental[122] range of 5.3-6.2 indicates an overestimate. The large value is due to the shoulder feature on the right of the first peak of the $g_{\mathrm{Cl--O}}$ radial distribution function. Inspections of snapshots indicates that the first solvation shell contains on average one water molecule that is not hydrogen bonded to the Cl$^-$ ion. Again this feature might be attributed to the presence of the H$^+$ cation in the second solvation shell.

The excess proton is associated with a single water molecule, forming H$_3$O$^+$ in approximately 70% of the time, and shared between two water molecules, forming a ${\rm H_5O^+_2}$ complex in approximately 30% of the time. This is in agreement with the CP-MD results of Tuckerman et al.[52,53], from their study of the solvation and transport of H$_3$O$^+$ in water at infinite dilution with 60% and 40% abundancies of the H$_3$O$^+$ and H$_5$O$_2^+$ hydronium complexes, respectively. (see for the criteria to distinguish between the complexes refs TLSP1 and TLSP2).

This difference might be attributed to the presence of the Cl$^-$ ion in our work. The water structure surrounding the hydronium complexes is very similar to their results, which follows from the comparison of the radial distribution functions (data not shown).

From the calculations of the gas phase structures and the preparatory AIMD simulations of water and dilute hydrochloric acid, we may conclude that our numerical approach, using DFT-BP together with the Car-Parrinello technique as implemented in the PAW method, yields results consistent with results reported in the literature. These results also confirm reports in the literature that the CP-MD method is able to reproduce properties of aqueous solutions with an acceptable accuracy. An important technical detail is that, for accuracies of 1 kcal/mol for the energies and 0.03 Å for bond lengths of the systems in this study, the plane wave basis set can be kept as small as a 30 Ry kinetic energy cutoff.