Appendix C: Coordination constraint as the reaction coordinate

Figure 3.8: Upper graph: the force of constraint shows a sudden jump at $t\approx 26$ in the AIMD run with $\xi =0.55$ (gray line). Lower graph: the difference in amounts of solvation for the leaving and attacking Cl groups $f_{\rm Cl'}-f_{\rm Cl}$, as defined by equation 3.12, shows a very similar behaviour, which confirms the strong coupling between the reactants and the aqueous solution. The black lines are running averages.

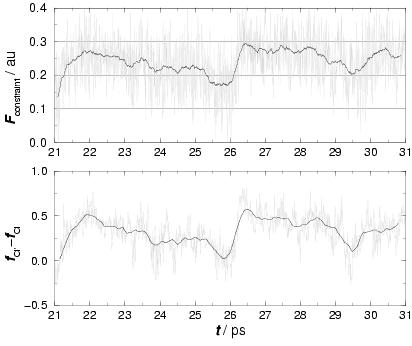
During the constrained AIMD simulation at $\xi =0.55$, a sudden jump in the force of constraint was observed, which is shown in the upper panel of figure 3.8 by the gray line and emphasized by the running average (black line). The jump indicates a fluctuation in the solvent environment around the [Cl$\cdots$CH$_3 \cdots$Cl]$^-$ complex, which could be a stepwise relaxation of the lagging behind Cl solvation shells to the new constrained reaction coordinate value $\xi =0.55$. Comparison of Cl coordination numbers and radial distribution functions before and after the sudden jump does not show significant modifications in the hydration, probably because the relevant solvent fluctuations are averaged out. We therefore computed a simple running function which counts all hydrogens around each Cl weighted by the square of the reciprocal Cl-H distance:

$$f_i(t) = \sum_j r^{-2}_{\rm {Cl}_i-\rm {H}_j} (t)$$ (58)

This function gives an indication of the number of water molecules in the neighborhood of a Cl and thus of the amount of Cl hydration. The difference of the amounts of hydration for both Cl's is plotted in the lower panel of figure 3.8, again with a running average in black. The figure indeed shows a strong correlation between the difference of Cl solvation and the force of constraint, confirming the expected strong reactant-solvent coupling (see also appendix 3.5).

Can we use this result to improve the reaction coordinate by including solvent degrees of freedom? Perhaps we can even control the S$_\mathrm{N}$2 reaction in aqueous solution completely by gradually switching on the amount of hydration on the leaving Cl and simultaneously switching off the amount of hydration on the attacking Cl, using a constrained reaction coordinate of the form $f_{\rm {Cl}^\prime} - f_{\rm {Cl}}$? Sprik proposed in 1998 such a coordination constraint using a fermi-dirac function of the solute-solvent distances to study the coordination in a lennard-jones argon liquid[126] and the (de-)protonation of H$_2$O in liquid water[127]. This approach and also his results indeed look very promising. However, we should note that a coordination constraint of this type does not fix the actual transition state of a process which involves a change in the coordination number. In other words, use of transition state theory will lead to a too low barrier so that one still has to perform the expensive compution of the transmission coefficient to compare with experiment.