Already in 1940, Hendrik Kramers understood well the mechanism of climbing
the reaction barrier in solution as governed by the thermal (Brownian) motions
of the solvent. The above mentioned rare event problem did not play a role
in the description he used, as the solvent effect was not described by explicit
molecules, but rather by Gaussian random fluctuations ![]() and by a linear friction
force
and by a linear friction
force
![]() working on a reaction coordinate
working on a reaction coordinate ![]() with a mass
with a mass ![]() .
A one-dimensional asymmetric double-well potential
.
A one-dimensional asymmetric double-well potential ![]() represents the
reactant and product well and the separating barrier along by the reaction
coordinate, which enter with the solvent forces Newton's equation of motion
of
represents the
reactant and product well and the separating barrier along by the reaction
coordinate, which enter with the solvent forces Newton's equation of motion
of ![]() in the form of a Langevin equation:
in the form of a Langevin equation:
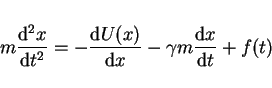 |
(11) |
Transition state theory[5] is based on two assumptions, namely
1) thermodynamic equilibrium must prevail throughout the entire system for
all degrees of freedom and 2) any transition pathway starting from the reactant state
which crosses the dividing transition state surface will end up in the product state.
For strong (over-damped) friction,
![]() , the expression for the
rate constant simplifies to,
, the expression for the
rate constant simplifies to,
![\begin{displaymath}
k_R = \frac{\omega_b}{\gamma} \frac{\omega_R}{2 \pi } \exp{[-\beta E_b]}
\end{displaymath}](img184.png) |
(14) |
In the low solvent friction limit, Kramers found
![\begin{displaymath}
k_R = p \gamma \frac{I(E_b^+)}{k_BT}
\Bigg\{\frac{\omega_R}{2\pi}\exp{[-\beta E_b^+]}\Bigg\}
\end{displaymath}](img189.png) |
(15) |
Kramers reaction rate theory predicts that the solvent dynamics will always
decrease the reaction rate, or that in the most favorable situation no barrier
recrossings take place and the rate constant corresponds with that of
Rice-Ramsperger-Kassel-Marcus (RRKM) rate theory, which gives the TST rate
as a function of the collision rate for independent polyatomic molecules.
However, for general realistic applications, Kramers' theory (and RRKM theory)
fails when the time scale of barrier crossing
(which is of course much faster than ![]() ) is in the same order or even slower than the time scale
of the correlations in the random solvent fluctuations. Moreover in RRKM theory,
the reacting polyatomic molecules provide there own (infinitely fast)
energy sinks, whereas in realistic applications the coupling of the reaction
coordinate with these intramolecular modes can be weaker than the coupling
(friction) with the solvent. In certain cases, the solvent dynamics can therefore
increase the reaction rate, as it provides an extra energy dissipation source
after barrier crossing.
An important improvement on Kramers formulation is the generalization to
non-Markovian solvents which introduces memory effects in the solvent fluctuations
expressed by equation 2.11 (Grote-Hynes theory[6]).
An excellent review of improvements on Kramers theory of barrier crossings
in many-particle systems is found in ref kramersreview90.
) is in the same order or even slower than the time scale
of the correlations in the random solvent fluctuations. Moreover in RRKM theory,
the reacting polyatomic molecules provide there own (infinitely fast)
energy sinks, whereas in realistic applications the coupling of the reaction
coordinate with these intramolecular modes can be weaker than the coupling
(friction) with the solvent. In certain cases, the solvent dynamics can therefore
increase the reaction rate, as it provides an extra energy dissipation source
after barrier crossing.
An important improvement on Kramers formulation is the generalization to
non-Markovian solvents which introduces memory effects in the solvent fluctuations
expressed by equation 2.11 (Grote-Hynes theory[6]).
An excellent review of improvements on Kramers theory of barrier crossings
in many-particle systems is found in ref kramersreview90.
From the phenomenological point of view, the Langevin equation and Fokker-Planck
equation methods to describe barrier crossings in the condensed phase have
been (and still are) very important for our understanding of solvent effects
on the rate constant. A disadvantage of these methods is that they depend
heavily on parameters such as the potential felt by the reaction coordinate ![]() ,
the coupling (friction) between the reactants and the solvent
,
the coupling (friction) between the reactants and the solvent ![]() and
the dissipative fluctuating force
and
the dissipative fluctuating force ![]() , which are not known for general applications.
Moreover, we are also interested in the behavior of the solvent environment
during a chemical reaction, which requires the inclusion of explicit molecules
via molecular dynamics.
We will therefore make use of an alternative microscopic expression for the
reaction rate derived from the macroscopic equations (2.1) for
which in equilibrium
, which are not known for general applications.
Moreover, we are also interested in the behavior of the solvent environment
during a chemical reaction, which requires the inclusion of explicit molecules
via molecular dynamics.
We will therefore make use of an alternative microscopic expression for the
reaction rate derived from the macroscopic equations (2.1) for
which in equilibrium
![]() .
We introduce a microscopic reaction coordinate
.
We introduce a microscopic reaction coordinate ![]() and the Heavyside
step-function
and the Heavyside
step-function
![]() which indicates whether the system finds itself
in the reactant state or in the product state,
which indicates whether the system finds itself
in the reactant state or in the product state,

| (16) | |||
| (17) |
|
In the shape of equation 2.17, apparently we still have to
perform one prohibitively long simulation and wait for every occasion that the
barrier top is reached to set our stopwatch to ![]() and add a measurement of
and add a measurement of
![]() to our statistics, in order to obtain
to our statistics, in order to obtain ![]() .
For practical calculations we therefore rewrite equation 2.17
by multiplying numerator and denominator with
.
For practical calculations we therefore rewrite equation 2.17
by multiplying numerator and denominator with
![]() , giving:
2pt
, giving:
2pt
The last term at right-hand-side of equation 2.18 is simply the
probability to find the system at the transition state relative to the
probability of finding the system in the reactant state. The term in the middle
gives the average forward crossing speed at the transition state, which
equals together with the last term the transition state theory rate
constant,
![]() . The first term at right-hand-side is again
the transmission function, which corrects upon
. The first term at right-hand-side is again
the transmission function, which corrects upon
![]() for long
enough correlation times
for long
enough correlation times ![]() , by giving the fraction of transitions that
end up in the product
state, irrespective of the crossing direction, relative to the fraction
that crosses in the forward direction. Or using Chandlers notation[10]:
, by giving the fraction of transitions that
end up in the product
state, irrespective of the crossing direction, relative to the fraction
that crosses in the forward direction. Or using Chandlers notation[10]:
![\begin{displaymath}
k_R = \kappa \frac{1}{2}\left< \left\vert \dot{x} \right\ver...
...-\infty}^{x^\ddagger} \mathrm{d}x \exp{[-\beta \Delta G(x)]} }
\end{displaymath}](img219.png) |
(20) |
The separated terms can in principle all be computed using molecular
dynamics. The transmission function ![]() , expressed by the time correlation
function in the first term of eqation 2.18, is usually obtained by
performing a dynamics run with the reaction coordinate constrained at the
transition state
, expressed by the time correlation
function in the first term of eqation 2.18, is usually obtained by
performing a dynamics run with the reaction coordinate constrained at the
transition state ![]() to obtain a large number of starting configurations
with a positive crossing velocity, which are then used to initiate unconstrained
MD runs to evaluate
to obtain a large number of starting configurations
with a positive crossing velocity, which are then used to initiate unconstrained
MD runs to evaluate
![]() . The average crossing
velocity (i.e. the second term) can be obtained from the initial
constrained run. The last term, the probability to reach the transition
state from the reactant state, can be obtained using a method to calculate
free energy differences, such as umbrella sampling[13,14,15]
or thermodynamic integration in combination with the method of
constraint[16]. In the umbrella sampling method,
the system is biased by addition of an (umbrella) potential
. The average crossing
velocity (i.e. the second term) can be obtained from the initial
constrained run. The last term, the probability to reach the transition
state from the reactant state, can be obtained using a method to calculate
free energy differences, such as umbrella sampling[13,14,15]
or thermodynamic integration in combination with the method of
constraint[16]. In the umbrella sampling method,
the system is biased by addition of an (umbrella) potential ![]() , which
approximately cancels the free energy barrier. In the MD run, the system
can now move barrier-free back and forth from the reactant state to the product
state. Accumulating the probability distribution
, which
approximately cancels the free energy barrier. In the MD run, the system
can now move barrier-free back and forth from the reactant state to the product
state. Accumulating the probability distribution ![]() gives the desired free
energy profile,
gives the desired free
energy profile,
![]() .
Using the method of constraint, one
performs a number of constrained MD runs at different constraint values of
the reaction coordinate. In each constrained run, one accumulates the force
required to keep the reaction coordinate fixed. The obtained average constraint forces
can be related to the thermodynamic force,
.
Using the method of constraint, one
performs a number of constrained MD runs at different constraint values of
the reaction coordinate. In each constrained run, one accumulates the force
required to keep the reaction coordinate fixed. The obtained average constraint forces
can be related to the thermodynamic force,
![]() , along the reaction
coordinate[17], so that integration gives the desired free energy profile.
, along the reaction
coordinate[17], so that integration gives the desired free energy profile.
Summarizing, we see that chemical reactions are activated processes,
and in particular that barrier crossings are, on the time scale of the thermal motions,
rare but very important events. Performing the reaction in solution affects
the reaction rate constant in two ways: 1) the static energy barrier is changed,
due to different energies of solvation for the reactant state and
the transition state (on the same ground the equilibrium constant ![]() can be changed by different energies of solvation for the reactant state and
the product state) and 2) the solvent dynamics can alter the rate by
providing an extra energy sink after barrier crossing (increasing
the rate constant) or by forcing the reactants into recrossings at the
barrier top region (decreasing the rate constant). By separating the rate
constant in terms of the probability to reach the barrier top, the crossing
velocity and the transmission coefficient, solvent effects on the reaction
rate constant can be studied with molecular dynamics techniques.
can be changed by different energies of solvation for the reactant state and
the product state) and 2) the solvent dynamics can alter the rate by
providing an extra energy sink after barrier crossing (increasing
the rate constant) or by forcing the reactants into recrossings at the
barrier top region (decreasing the rate constant). By separating the rate
constant in terms of the probability to reach the barrier top, the crossing
velocity and the transmission coefficient, solvent effects on the reaction
rate constant can be studied with molecular dynamics techniques.