The number of different configurations of positions ![]() and momenta
and momenta
![]() of
of ![]() particles in a volume
particles in a volume ![]() at an absolute temperature
at an absolute temperature ![]() is for all but the simplest systems mindbogglingly large. In the canonical
ensemble (i.e. at fixed
is for all but the simplest systems mindbogglingly large. In the canonical
ensemble (i.e. at fixed ![]() ,
,![]() , and
, and ![]() ), the probability
), the probability ![]() to find the
system in some configuration (
to find the
system in some configuration (
![]() ) depends on the total energy
of the configuration given by the Hamiltonian
) depends on the total energy
of the configuration given by the Hamiltonian
![]() according to the Boltzmann distribution:
according to the Boltzmann distribution:
![\begin{displaymath}
\left<a\right> = \frac{\int\!\!\int \mathrm{d}{\bf r}^N\!\ma...
...athrm{d}{\bf p}^N
\exp[-\beta {\cal H}({\bf r}^N, {\bf p}^N)]}
\end{displaymath}](img154.png) |
(7) |
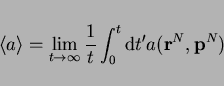 |
(8) |
An advantage of MD over Monte Carlo is that also dynamical properties
can be evaluated. Onsager's regression hypothesis states that
slow microscopic fluctuations around equilibrium on average decay according to
the macroscopic laws.[3] For example, transport properties such as
the diffusion coefficient
of some species ![]() ,
, ![]() , which is the macroscopic proportionality constant between
the flux
, which is the macroscopic proportionality constant between
the flux ![]() of the diffusing species
of the diffusing species ![]() and the gradient of its concentration
and the gradient of its concentration
![]() as given by Fick's law,
as given by Fick's law,
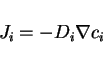 |
(9) |
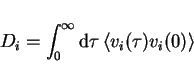 |
(10) |
Simulation of a chemical reaction and therefore the direct estimation of the
rate constant ![]() is in practice not possible using MD or Monte Carlo.
The problem is, that for the system to move from the stable reactant state
to the stable product state, it has to cross some transition state
configuration associated with the relatively high activation energy,
is in practice not possible using MD or Monte Carlo.
The problem is, that for the system to move from the stable reactant state
to the stable product state, it has to cross some transition state
configuration associated with the relatively high activation energy,
![]() , of equation 2.2, which has a very
low probability of being populated during a simulation, as follows from
the exponential dependence in equation 2.4. This dynamical
bottleneck makes the chemical
reaction a rare event on the time scale of the thermal motions.
Fortunately, there are a number of techniques available to circumvent this
problem.
, of equation 2.2, which has a very
low probability of being populated during a simulation, as follows from
the exponential dependence in equation 2.4. This dynamical
bottleneck makes the chemical
reaction a rare event on the time scale of the thermal motions.
Fortunately, there are a number of techniques available to circumvent this
problem.