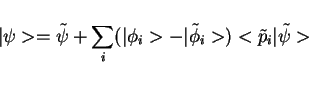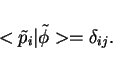


Next: Density Functional Theory
Up: Techniques
Previous: Reaction rate theory
Contents
Car-Parrinello molecular dynamics
The motion of small, but not too small, particles such as atoms and
molecules is usually well described by Lagrangian mechanics, with the
Lagrangian 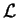 defined
as the kinetic energy minus the potential energy,
defined
as the kinetic energy minus the potential energy,
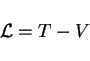 |
(21) |
leading to the set of Newtonian equations of motion for each particle 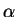 ,
with mass
,
with mass 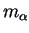 and cartesian coordinate
and cartesian coordinate
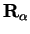 :
:
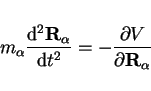 |
(22) |
Numerical integration of the equations of motion, taking small time steps
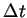 , results in a trajectory through the hyper-space of all possible
positions and momenta of the particles, called phase-space. This simulation
technique is known as molecular dynamics (MD).
, results in a trajectory through the hyper-space of all possible
positions and momenta of the particles, called phase-space. This simulation
technique is known as molecular dynamics (MD).
The motion of even smaller particles, such as electrons, cannot be
approximated with classical Newtonian dynamics, but instead has to
be described with the more accurate quantum mechanical equations of motion
derived from the time-independent Schrödinger equation:
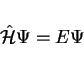 |
(23) |
That is, the Hamiltonian
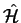 , given as the sum of the
kinetic and potential energy operators, operating on the many-electron
wave function
, given as the sum of the
kinetic and potential energy operators, operating on the many-electron
wave function 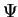 gives us the energy
gives us the energy 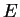 . This rather simple and
very famous equation can unfortunately not be solved analytically
for a system of more than two electrons, and approximations on the
Hamiltonian have to be introduced. Following Kohn and Sham's
density functional theory (DFT) approach (see next section for
the details on DFT), the exact density and the exact energy can be obtained from
one-electron wave functions, the Kohn-Sham (KS) orbitals
. This rather simple and
very famous equation can unfortunately not be solved analytically
for a system of more than two electrons, and approximations on the
Hamiltonian have to be introduced. Following Kohn and Sham's
density functional theory (DFT) approach (see next section for
the details on DFT), the exact density and the exact energy can be obtained from
one-electron wave functions, the Kohn-Sham (KS) orbitals 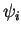 ,
which are solutions in a local potential. The heart of this machinery
lies in the notion that all properties, including the energy,
of the electronic system are a functional of the electron density,
,
which are solutions in a local potential. The heart of this machinery
lies in the notion that all properties, including the energy,
of the electronic system are a functional of the electron density, 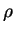 ,
,
![\begin{displaymath}
E=E[\rho]
\end{displaymath}](img237.png) |
(24) |
The Kohn-Sham orbitals
can be expanded in an orthogonal basis
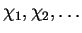 :
:
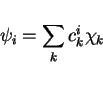 |
(25) |
with 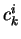 the expansion coefficients. The electron density
the expansion coefficients. The electron density 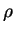 ,
given as
,
given as
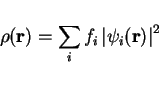 |
(26) |
with 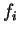 the occupation number of KS orbital
the occupation number of KS orbital 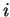 , gives us the probability
to find an electron at position
, gives us the probability
to find an electron at position 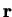 .
.
In DFT, the sets of coefficients 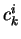 span a hyper-space
span a hyper-space 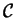 , in which
a point representing orthonormal KS orbitals
, in which
a point representing orthonormal KS orbitals 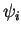 thus corresponds to an energy
thus corresponds to an energy 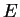 , similar to a point in atomic coordinate
space corresponding to a potential energy
, similar to a point in atomic coordinate
space corresponding to a potential energy 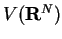 . In fact, the iterative search
for the one point in
. In fact, the iterative search
for the one point in 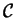 that minimizes the energy to the physical ground-state
energy
that minimizes the energy to the physical ground-state
energy 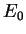 , resembles a molecular geometry optimization to minimize the
potential energy. Since we want the one-electron functions
, resembles a molecular geometry optimization to minimize the
potential energy. Since we want the one-electron functions 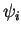 to
be orthonormal, the trajectory through
to
be orthonormal, the trajectory through 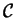 during the energy minimization
is constrained on a hyper-surface in
during the energy minimization
is constrained on a hyper-surface in 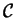 for which
for which
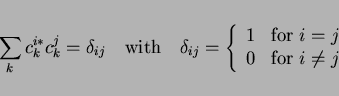 |
(27) |
Taking the iteration steps as the analog of time steps, we can even formulate
Newtonian equations of motion for the ``dynamics'' of changing coefficients:
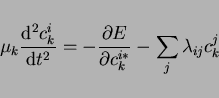 |
(28) |
Here, the 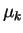 are inertia parameters, usually called ``fictitious masses'',
which control the acceleration of the coefficients,
are inertia parameters, usually called ``fictitious masses'',
which control the acceleration of the coefficients,
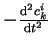 due to the force on the coefficients,
on the right-hand-side. The last term arises from the constraint
in equation 2.26, with
due to the force on the coefficients,
on the right-hand-side. The last term arises from the constraint
in equation 2.26, with 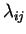 the undetermined
Lagrange multipliers. The forces on the coefficients are given as
the undetermined
Lagrange multipliers. The forces on the coefficients are given as
![\begin{displaymath}
- \frac{\partial E[\{c_k^i\},\{ {\bf R}_\alpha \}] }{\partial c_k^i } =
- \sum_l n_i H^\mathrm{KS}_{kl} c_l^i
\end{displaymath}](img252.png) |
(29) |
which can amount to a considerable saving of computer time and memory with respect
to techniques based on diagonalization of the full Hamiltonian matrix.
In practice, the wave function coefficients are not known
a priori, and we start from a random set of 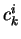 , consistent with
equation 2.26, associated with a
meaningless energy
, consistent with
equation 2.26, associated with a
meaningless energy 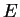 via equations 2.23 and 2.24.
When we start to integrate the equations of motion (eq. 2.27),
the coefficients will accelerate towards configurations with lower energies
and gain ``kinetic energy'', until a dynamic equilibrium is reached. The
electronic ground-state energy
via equations 2.23 and 2.24.
When we start to integrate the equations of motion (eq. 2.27),
the coefficients will accelerate towards configurations with lower energies
and gain ``kinetic energy'', until a dynamic equilibrium is reached. The
electronic ground-state energy 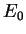 is found by damping the coefficient
dynamics, so that kinetic energy is gradually removed and the coefficients
eventually freeze in the ground-state configuration. This technique to optimize
the wave function is known as ``simulated annealing''.
is found by damping the coefficient
dynamics, so that kinetic energy is gradually removed and the coefficients
eventually freeze in the ground-state configuration. This technique to optimize
the wave function is known as ``simulated annealing''.
Car-Parrinello molecular dynamics (CPMD) is the integration of the fictitious wave
function coefficient dynamics with the classical molecular dynamics by a
single extended Lagrangian.
Starting from some atomic configuration in the
(optimized) electronic ground-state, we can calculate the forces on the
atoms using the Hellmann-Feynman theorem,
![\begin{displaymath}
- \frac{\partial E[\{c_k^i\},\{ {\bf R}_\alpha \}] }{\partia...
... {\cal H}}{\partial {\bf R}_\alpha }
\left\vert \Psi \right >
\end{displaymath}](img257.png) |
(31) |
to start the ab initio molecular dynamics. Initially,
the forces on the coefficients equal zero as the electronic configuration is
at its minimum, but after one time step the atomic positions have changed and
the wave function is no longer up to date. However, since the electronic
degrees of freedom 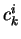 and the atomic positions
and the atomic positions
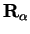 are coupled
via the potential energy (equation 2.29), the forces on the
coefficients are no longer zero and the coefficients accelerate towards the
new electronic ground-state. When the fictitious coefficient masses
are coupled
via the potential energy (equation 2.29), the forces on the
coefficients are no longer zero and the coefficients accelerate towards the
new electronic ground-state. When the fictitious coefficient masses 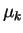 are chosen sufficiently small (i.e.
are chosen sufficiently small (i.e.
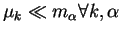 )
the response of the coefficients to the changing nuclei
)
the response of the coefficients to the changing nuclei  is so
rapid that the electrons remain to a sufficiently high degree in the
ground-state.
is so
rapid that the electrons remain to a sufficiently high degree in the
ground-state.
Figure 2.2:
Vibrational spectrum of the normal modes of the electronic
coefficients (solid line) for a system with a large gap (periodic super cell
containing 8 Si atoms in the diamond structure). The solid triangle indicates
the position of the highest ionic frequency. The vertical bars below the spectrum
represent the frequencies obtained from equation 2.31.
Figure from ref PaSmBu91.
|
|
Of course, the dynamics of the nuclei in CPMD has only physical meaning if
the electronic structure is close to its instantaneous ground-state at each
step of the simulation. In other words, the dynamics of the electronic coefficients
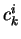 has to remain relatively cold. However, since the two dynamic sub-systems
of nuclei
has to remain relatively cold. However, since the two dynamic sub-systems
of nuclei
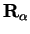 and electronic coefficients
and electronic coefficients 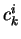 are coupled, in principle
energy can flow from the relatively hot nuclei sub-system, to the colder
coefficients, which would lead to deviations from the Born-Oppenheimer (ground-state)
surface. In many practical simulations, the energy flow between the sub-systems can
be suppressed with a good choice for the fictitious coefficient masses
are coupled, in principle
energy can flow from the relatively hot nuclei sub-system, to the colder
coefficients, which would lead to deviations from the Born-Oppenheimer (ground-state)
surface. In many practical simulations, the energy flow between the sub-systems can
be suppressed with a good choice for the fictitious coefficient masses 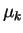 ,
which can be rationalized by regarding the electronic coefficient dynamics
for small deviations from the ground-state, described as a superposition of
harmonic oscillations whose frequency is given by:
,
which can be rationalized by regarding the electronic coefficient dynamics
for small deviations from the ground-state, described as a superposition of
harmonic oscillations whose frequency is given by:
Here, 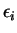 indicates the eigenvalue of the
indicates the eigenvalue of the 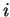 th unoccupied and
th unoccupied and
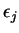 the
the 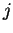 th occupied level, and the fictitious coefficient
masses
th occupied level, and the fictitious coefficient
masses 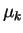 are chosen equal for all
are chosen equal for all 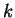 .
As an illustration, let us refer to figure 2.2 from
the illuminating study of ref PaSmBu91, which shows the vibrational density
of states of the electronic coefficients for an unrealistic but instructive
model of crystalline silicon. The fictitious mass in this work was
.
As an illustration, let us refer to figure 2.2 from
the illuminating study of ref PaSmBu91, which shows the vibrational density
of states of the electronic coefficients for an unrealistic but instructive
model of crystalline silicon. The fictitious mass in this work was 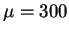 au.
The solid line is obtained from the Fourier transform of the velocity
autocorrelation function
au.
The solid line is obtained from the Fourier transform of the velocity
autocorrelation function
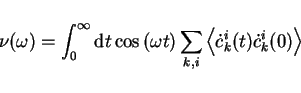 |
(33) |
from a simulation of 3000 time steps (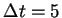 au) and the vertical bars below
are obtained from equation 2.31. The lowest electronic
frequency (at about 1010 THz) results from the energy gap, which is in this model
au) and the vertical bars below
are obtained from equation 2.31. The lowest electronic
frequency (at about 1010 THz) results from the energy gap, which is in this model
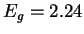 eV, in good agreement with the estimate using
equation 2.31:
eV, in good agreement with the estimate using
equation 2.31:
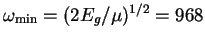 THz.
The highest ionic frequency for this model is 140 THz, indicated by the triangle
in figure 2.2. This clear separation between the characteristic
electronic and ionic frequencies, is the reason that the irreversible energy
transfer from the slow to the fast degrees of freedom is minimal, and the main
reason that CPMD works! Problems occur for systems with a small or vanishing
bandgap, such as semiconductors and metals, because the heat transfer can no longer
be controlled by choosing a small enough
THz.
The highest ionic frequency for this model is 140 THz, indicated by the triangle
in figure 2.2. This clear separation between the characteristic
electronic and ionic frequencies, is the reason that the irreversible energy
transfer from the slow to the fast degrees of freedom is minimal, and the main
reason that CPMD works! Problems occur for systems with a small or vanishing
bandgap, such as semiconductors and metals, because the heat transfer can no longer
be controlled by choosing a small enough 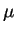 . A workable solution for these
systems can be provided by coupling both dynamical sub-systems to thermostats
which remove kinetic energy from the electronic coefficients while adding kinetic
energy to the nuclei[19].
. A workable solution for these
systems can be provided by coupling both dynamical sub-systems to thermostats
which remove kinetic energy from the electronic coefficients while adding kinetic
energy to the nuclei[19].
As the electronic coefficients rapidly fluctuate
around their optimal values, the instantaneous values of the forces do not
coincide with the Hellmann-Feynmann forces, however their average values do to
a very high degree of accuracy. The high efficiency of the Car-Parrinello
approach with respect to the so-called (real-) Born-Oppenheimer molecular dynamics
(BOMD) method also lies in this respect. In BOMD, the electronic structure is
self-consistently optimized after each time step in which only the relatively
small number of nuclei positions are propagated. In practice, the convergence
of the optimization has to be very high to avoid the accumulation of the small, but
systematic (!), deviations in the Hellmann-Feynman forces, which makes BOMD
computational more demanding than CPMD. This difference in efficiency is
partly reduced by the larger time step that can be used in BOMD, as the
maximum time step is limited by the proper integration of the equation of motions
of the fastest (i.e. lightest) particles, which are the high frequency
components of the fictitious dynamics in CPMD, whereas in BOMD, the lightest nuclei
limit the time step maximum.
A technique to accelerate CPMD further is known as
mass-preconditioning[20], which is based on reducing these high
frequency components of the fictitious dynamics by properly scaling the
fictitious masses 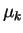 , so that a larger time step can be used.
Excellent reviews of the Car-Parrinello molecular dynamics techniques are
found in refs MaHuReview,ReMaReview,GaPaReview.
, so that a larger time step can be used.
Excellent reviews of the Car-Parrinello molecular dynamics techniques are
found in refs MaHuReview,ReMaReview,GaPaReview.
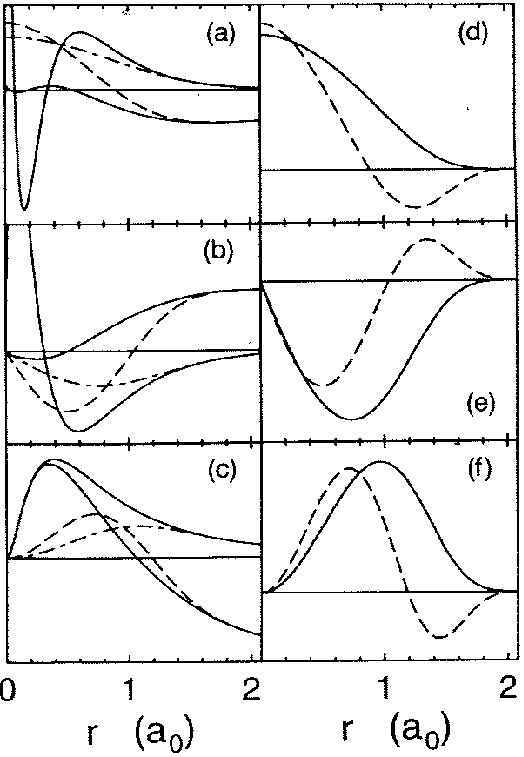
Figure 2.3:
Partial waves and projectors for Mn. Left panel:
partial waves 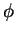 (solid lines) and pseudo partial waves
(solid lines) and pseudo partial waves 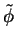 (dashed
and dash-dotted lines). The ``first'' pseudo partial wave is a dash-dotted line.
Right panel: first (solid line) and second (dashed line) projector functions. (a)
and (d) show the results for the first and second partial wave of the
(dashed
and dash-dotted lines). The ``first'' pseudo partial wave is a dash-dotted line.
Right panel: first (solid line) and second (dashed line) projector functions. (a)
and (d) show the results for the first and second partial wave of the 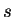 angular
momentum channel, respectively, (b) and (e) for the
angular
momentum channel, respectively, (b) and (e) for the 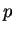 channel and (c) and (f)
for the
channel and (c) and (f)
for the 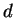 channel. 3
channel. 3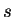 and 3
and 3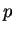 functions are treated as valence states.
Figure from ref PAW.
functions are treated as valence states.
Figure from ref PAW.
|
|
The first CPMD implementations used a basis set of plane waves, in combination
with a pseudopotential[25,26,27], to expand the
one-electron valence wave functions,
which is the most widely used approach in electronic structure calculations in
the field of solid state physics. Plane waves are of the form
![$\psi=N^{-1}\exp{[i{\bf Gr}]}$](img273.png) (
(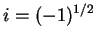 and
and 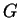 the wave vector), which are
the eigenfunctions of Schrödinger's equation (2.22) for
an electron in vacuum with kinetic energy
the wave vector), which are
the eigenfunctions of Schrödinger's equation (2.22) for
an electron in vacuum with kinetic energy
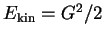 . For
electrons in an external field, such as in atoms, however, an expansion in
plane waves is a rather poor choice, because these functions hardly mimic
the rapid fluctuations of the one-electron wave functions in the neighborhood
of the nucleus. Usually the low lying core electrons are kept "frozen" during
an electronic structure calculation to reduce the computational cost, which is
a good approximation since these states remain practically invariant from
their atomic ground-state during the chemistry of bond breaking and making.
For the chemically active valence wave functions a pseudopotential is used
to describe the inner region (nucleus plus core electrons) of the atom, in a way that
allows for replacing the rapid fluctuating functions by more smooth functions.
Beyond this inner region, the smooth functions agree with the true wave functions.
A disadvantage of the pseudopotential method is that they become "very hard"
for first row elements and for systems with
. For
electrons in an external field, such as in atoms, however, an expansion in
plane waves is a rather poor choice, because these functions hardly mimic
the rapid fluctuations of the one-electron wave functions in the neighborhood
of the nucleus. Usually the low lying core electrons are kept "frozen" during
an electronic structure calculation to reduce the computational cost, which is
a good approximation since these states remain practically invariant from
their atomic ground-state during the chemistry of bond breaking and making.
For the chemically active valence wave functions a pseudopotential is used
to describe the inner region (nucleus plus core electrons) of the atom, in a way that
allows for replacing the rapid fluctuating functions by more smooth functions.
Beyond this inner region, the smooth functions agree with the true wave functions.
A disadvantage of the pseudopotential method is that they become "very hard"
for first row elements and for systems with 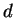 and
and 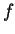 electrons, so that
very large basis sets are required. An improvement on the traditional
pseudopotentials was provided with the development of Vanderbilt's ultrasoft
pseudopotentials [28,29] by relaxing on the norm conserving
condition that is usually imposed.
The simulations described in this thesis were performed with Blöchl's
CPMD implementation, named projector augmented wave or PAW[24],
which is based on a generalization of both the pseudopotential approach and the
linear augmented-plane wave method[30,31,32] (LAPW).
In contrast to the pseudopotential approach, the LAPW technique utilizes
the full one-electron valence wave function with the correct nodal structure.
The wave function is subdivided into two regions; an inner (augmentation) region,
which is expanded in a basis set of localized functions, and an outer region
which is described by plane waves. At a certain (muffin-tin) sphere radius
from the nucleus, the partial wave functions are matched together by value
and derivative of the functions.
Instead in PAW, a linear transformation between the one-electron valence wave functions
electrons, so that
very large basis sets are required. An improvement on the traditional
pseudopotentials was provided with the development of Vanderbilt's ultrasoft
pseudopotentials [28,29] by relaxing on the norm conserving
condition that is usually imposed.
The simulations described in this thesis were performed with Blöchl's
CPMD implementation, named projector augmented wave or PAW[24],
which is based on a generalization of both the pseudopotential approach and the
linear augmented-plane wave method[30,31,32] (LAPW).
In contrast to the pseudopotential approach, the LAPW technique utilizes
the full one-electron valence wave function with the correct nodal structure.
The wave function is subdivided into two regions; an inner (augmentation) region,
which is expanded in a basis set of localized functions, and an outer region
which is described by plane waves. At a certain (muffin-tin) sphere radius
from the nucleus, the partial wave functions are matched together by value
and derivative of the functions.
Instead in PAW, a linear transformation between the one-electron valence wave functions
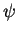 and fictitious pseudo wave functions
and fictitious pseudo wave functions 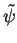 is used, in Dirac's
bra and ket notation:
is used, in Dirac's
bra and ket notation:
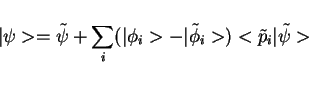 |
(34) |
where 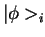 are a complete set of partial waves (
are a complete set of partial waves (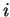 referring to the
atomic site
referring to the
atomic site 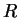 , the angular momentum quantum numbers
, the angular momentum quantum numbers 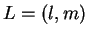 and the index
and the index 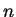 for different partial waves per
for different partial waves per 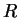 and
and 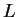 ). Each partial wave
). Each partial wave 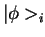 is
connected to a pseudo partial wave
is
connected to a pseudo partial wave
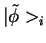 , which only differs from
, which only differs from
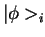 inside an augmentation region
inside an augmentation region 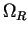 , and a localized, so-called,
projector function
, and a localized, so-called,
projector function 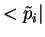 for which,
for which,
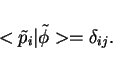 |
(35) |
As an illustration, we use figure 2.3 from ref PAW,
which shows the partial waves and projector functions for manganese.
The partial waves are functions on a radial grid, multiplied with spherical
harmonics, which are obtained by radially integrating Schrödinger's equation
for the isolated atom. The pseudo wave functions 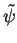 are expanded
in plane waves. In practice, the partial waves
are expanded
in plane waves. In practice, the partial waves 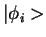 and
and
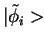 and
the projector functions
and
the projector functions 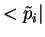 are imported from an atomic calculation at
the start of a PAW molecular dynamics calculation.
The main advantages of the PAW approach compared to the conventional norm-conserving
pseudopotential methods is that the atomic partial and projector functions are better
transferable than pseudopotentials and that the full wave function is accessible, which
allows for the calculation of core dependent quantities such as
hyperfine parameters and electric field gradients[33,34].
Also a smaller plane wave basis set is required than with the norm conserving
pseudopotential methods, which is most important for the present study as it
cuts heavily on the computational expense.
A very detailed description of the PAW technique and its relation to the traditional
norm conserving pseudopotential method and the LAPW method is found
in reference PAW.
are imported from an atomic calculation at
the start of a PAW molecular dynamics calculation.
The main advantages of the PAW approach compared to the conventional norm-conserving
pseudopotential methods is that the atomic partial and projector functions are better
transferable than pseudopotentials and that the full wave function is accessible, which
allows for the calculation of core dependent quantities such as
hyperfine parameters and electric field gradients[33,34].
Also a smaller plane wave basis set is required than with the norm conserving
pseudopotential methods, which is most important for the present study as it
cuts heavily on the computational expense.
A very detailed description of the PAW technique and its relation to the traditional
norm conserving pseudopotential method and the LAPW method is found
in reference PAW.



Next: Density Functional Theory
Up: Techniques
Previous: Reaction rate theory
Contents
Bernd Ensing
2003-06-13
![]() defined
as the kinetic energy minus the potential energy,
defined
as the kinetic energy minus the potential energy,
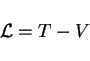
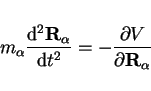
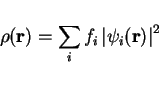
![]() span a hyper-space
span a hyper-space ![]() , in which
a point representing orthonormal KS orbitals
, in which
a point representing orthonormal KS orbitals ![]() thus corresponds to an energy
thus corresponds to an energy ![]() , similar to a point in atomic coordinate
space corresponding to a potential energy
, similar to a point in atomic coordinate
space corresponding to a potential energy ![]() . In fact, the iterative search
for the one point in
. In fact, the iterative search
for the one point in ![]() that minimizes the energy to the physical ground-state
energy
that minimizes the energy to the physical ground-state
energy ![]() , resembles a molecular geometry optimization to minimize the
potential energy. Since we want the one-electron functions
, resembles a molecular geometry optimization to minimize the
potential energy. Since we want the one-electron functions ![]() to
be orthonormal, the trajectory through
to
be orthonormal, the trajectory through ![]() during the energy minimization
is constrained on a hyper-surface in
during the energy minimization
is constrained on a hyper-surface in ![]() for which
for which
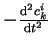 due to the force on the coefficients,
on the right-hand-side. The last term arises from the constraint
in equation 2.26, with
due to the force on the coefficients,
on the right-hand-side. The last term arises from the constraint
in equation 2.26, with 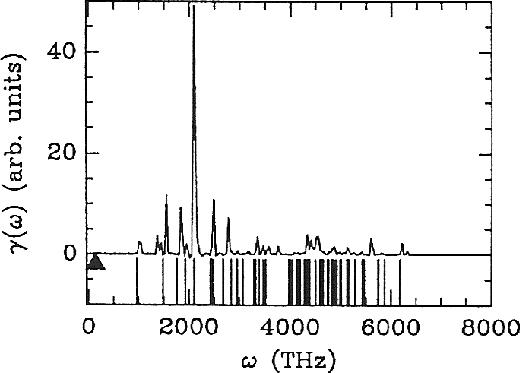
![]() has to remain relatively cold. However, since the two dynamic sub-systems
of nuclei
has to remain relatively cold. However, since the two dynamic sub-systems
of nuclei
![]() and electronic coefficients
and electronic coefficients ![]() are coupled, in principle
energy can flow from the relatively hot nuclei sub-system, to the colder
coefficients, which would lead to deviations from the Born-Oppenheimer (ground-state)
surface. In many practical simulations, the energy flow between the sub-systems can
be suppressed with a good choice for the fictitious coefficient masses
are coupled, in principle
energy can flow from the relatively hot nuclei sub-system, to the colder
coefficients, which would lead to deviations from the Born-Oppenheimer (ground-state)
surface. In many practical simulations, the energy flow between the sub-systems can
be suppressed with a good choice for the fictitious coefficient masses ![]() ,
which can be rationalized by regarding the electronic coefficient dynamics
for small deviations from the ground-state, described as a superposition of
harmonic oscillations whose frequency is given by:
,
which can be rationalized by regarding the electronic coefficient dynamics
for small deviations from the ground-state, described as a superposition of
harmonic oscillations whose frequency is given by:
![]() , so that a larger time step can be used.
Excellent reviews of the Car-Parrinello molecular dynamics techniques are
found in refs MaHuReview,ReMaReview,GaPaReview.
, so that a larger time step can be used.
Excellent reviews of the Car-Parrinello molecular dynamics techniques are
found in refs MaHuReview,ReMaReview,GaPaReview.
![]() (
(![]() and
and ![]() the wave vector), which are
the eigenfunctions of Schrödinger's equation (2.22) for
an electron in vacuum with kinetic energy
the wave vector), which are
the eigenfunctions of Schrödinger's equation (2.22) for
an electron in vacuum with kinetic energy
![]() . For
electrons in an external field, such as in atoms, however, an expansion in
plane waves is a rather poor choice, because these functions hardly mimic
the rapid fluctuations of the one-electron wave functions in the neighborhood
of the nucleus. Usually the low lying core electrons are kept "frozen" during
an electronic structure calculation to reduce the computational cost, which is
a good approximation since these states remain practically invariant from
their atomic ground-state during the chemistry of bond breaking and making.
For the chemically active valence wave functions a pseudopotential is used
to describe the inner region (nucleus plus core electrons) of the atom, in a way that
allows for replacing the rapid fluctuating functions by more smooth functions.
Beyond this inner region, the smooth functions agree with the true wave functions.
A disadvantage of the pseudopotential method is that they become "very hard"
for first row elements and for systems with
. For
electrons in an external field, such as in atoms, however, an expansion in
plane waves is a rather poor choice, because these functions hardly mimic
the rapid fluctuations of the one-electron wave functions in the neighborhood
of the nucleus. Usually the low lying core electrons are kept "frozen" during
an electronic structure calculation to reduce the computational cost, which is
a good approximation since these states remain practically invariant from
their atomic ground-state during the chemistry of bond breaking and making.
For the chemically active valence wave functions a pseudopotential is used
to describe the inner region (nucleus plus core electrons) of the atom, in a way that
allows for replacing the rapid fluctuating functions by more smooth functions.
Beyond this inner region, the smooth functions agree with the true wave functions.
A disadvantage of the pseudopotential method is that they become "very hard"
for first row elements and for systems with ![]() and
and ![]() electrons, so that
very large basis sets are required. An improvement on the traditional
pseudopotentials was provided with the development of Vanderbilt's ultrasoft
pseudopotentials [28,29] by relaxing on the norm conserving
condition that is usually imposed.
The simulations described in this thesis were performed with Blöchl's
CPMD implementation, named projector augmented wave or PAW[24],
which is based on a generalization of both the pseudopotential approach and the
linear augmented-plane wave method[30,31,32] (LAPW).
In contrast to the pseudopotential approach, the LAPW technique utilizes
the full one-electron valence wave function with the correct nodal structure.
The wave function is subdivided into two regions; an inner (augmentation) region,
which is expanded in a basis set of localized functions, and an outer region
which is described by plane waves. At a certain (muffin-tin) sphere radius
from the nucleus, the partial wave functions are matched together by value
and derivative of the functions.
Instead in PAW, a linear transformation between the one-electron valence wave functions
electrons, so that
very large basis sets are required. An improvement on the traditional
pseudopotentials was provided with the development of Vanderbilt's ultrasoft
pseudopotentials [28,29] by relaxing on the norm conserving
condition that is usually imposed.
The simulations described in this thesis were performed with Blöchl's
CPMD implementation, named projector augmented wave or PAW[24],
which is based on a generalization of both the pseudopotential approach and the
linear augmented-plane wave method[30,31,32] (LAPW).
In contrast to the pseudopotential approach, the LAPW technique utilizes
the full one-electron valence wave function with the correct nodal structure.
The wave function is subdivided into two regions; an inner (augmentation) region,
which is expanded in a basis set of localized functions, and an outer region
which is described by plane waves. At a certain (muffin-tin) sphere radius
from the nucleus, the partial wave functions are matched together by value
and derivative of the functions.
Instead in PAW, a linear transformation between the one-electron valence wave functions
![]() and fictitious pseudo wave functions
and fictitious pseudo wave functions ![]() is used, in Dirac's
bra and ket notation:
is used, in Dirac's
bra and ket notation: