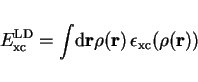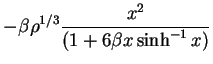


Next: Solvation effects on the
Up: Techniques
Previous: Car-Parrinello molecular dynamics
Contents
Density Functional Theory
In the previous section, we have shown that the ``simulated
annealing'' technique can be used to minimize the electronic energy of
a system by optimizing the electronic degrees of freedom, the
coefficients 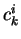 , or to minimize the atomic potential energy by
optimizing the atomic degrees of freedom, the positions
, or to minimize the atomic potential energy by
optimizing the atomic degrees of freedom, the positions
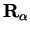 .
But we have not yet introduced the quantum mechanical relation between
the energy and the electronic coefficients and atomic positions,
to obtain the forces on the atoms and coefficients (eq. 2.30).
The reason is, that in principle various quantum mechanical (or even
semi-empirical methods) can be used, such as the Hartree-Fock method
or the configurational interaction method. Hartree-Fock, however, lacks
for many practical systems the desired chemical accuracy while on the
other hand the configurational interaction method, although it can be highly
accurate, is unpractical due to its dramatic scaling of the computational
expense with the number of electrons.
In practice, therefore, the energy and the forces are obtained
from an electronic structure calculation using density functional
theory (DFT), which is both accurate and has a favorable scaling.
.
But we have not yet introduced the quantum mechanical relation between
the energy and the electronic coefficients and atomic positions,
to obtain the forces on the atoms and coefficients (eq. 2.30).
The reason is, that in principle various quantum mechanical (or even
semi-empirical methods) can be used, such as the Hartree-Fock method
or the configurational interaction method. Hartree-Fock, however, lacks
for many practical systems the desired chemical accuracy while on the
other hand the configurational interaction method, although it can be highly
accurate, is unpractical due to its dramatic scaling of the computational
expense with the number of electrons.
In practice, therefore, the energy and the forces are obtained
from an electronic structure calculation using density functional
theory (DFT), which is both accurate and has a favorable scaling.
Density functional theory is based on the notion that for a many-electron
system there is a one-to-one mapping between the external potential and the
electron density:
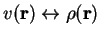 .
In other words, the density is uniquely determined given a potential,
and vice versa. All properties are therefore a functional of the
density, because the density determines the potential, which
determines the Hamiltonian, which determines the energy
(
.
In other words, the density is uniquely determined given a potential,
and vice versa. All properties are therefore a functional of the
density, because the density determines the potential, which
determines the Hamiltonian, which determines the energy
(![$E[\rho]$](img291.png) ) and the wave function (
) and the wave function (![$\Psi[\rho]$](img292.png) ), from which
all physical properties can be determined. This theorem was proven
in 1964 by Hohenberg and Kohn, using the variational principle
for systems with a non-degenerate ground-state. Hohenberg and Kohn
also showed that for a given potential
), from which
all physical properties can be determined. This theorem was proven
in 1964 by Hohenberg and Kohn, using the variational principle
for systems with a non-degenerate ground-state. Hohenberg and Kohn
also showed that for a given potential 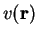 , which corresponds
with a ground-state
, which corresponds
with a ground-state ![$\Psi_0[\rho]$](img294.png) and ground-state energy
and ground-state energy ![$E_0[\rho]$](img295.png) ,
the energy functional
,
the energy functional ![$E_v[\rho]$](img296.png) has its minimum equal to
has its minimum equal to ![$E_0[\rho]$](img295.png) at the ground-state density (second Hohenberg-Kohn theorem), or:
at the ground-state density (second Hohenberg-Kohn theorem), or:
![\begin{displaymath}
\left< \Psi[\rho] \left \vert {\hat {\cal H}} \right\vert \P...
...r}) + T[\rho] + V_\mathrm{ee}[\rho] =
E_v[\rho] \ge E_0[\rho]
\end{displaymath}](img297.png) |
(36) |
with ![$T[\rho]$](img298.png) the electronic kinetic energy functional and
the electronic kinetic energy functional and
![$V_\mathrm{ee}[\rho]$](img299.png) the electron-electron interaction energy functional.
the electron-electron interaction energy functional.
A prescription to obtain the energy from the 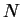 -electron density
was given by Kohn and Sham in a one-electron formalism, posing
that there exists an auxiliary system of
-electron density
was given by Kohn and Sham in a one-electron formalism, posing
that there exists an auxiliary system of 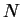 non-interacting
electrons, feeling only a local potential
non-interacting
electrons, feeling only a local potential 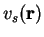 which
yields exactly the same density as the system of interacting
electrons with potential
which
yields exactly the same density as the system of interacting
electrons with potential 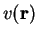 . The electron density is
represented by the sum of the densities of the
. The electron density is
represented by the sum of the densities of the 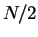 doubly occupied
single-particle spatial orbitals,
doubly occupied
single-particle spatial orbitals,
and the Kohn-Sham (KS) expression for the electronic energy functional
is given by:
![\begin{displaymath}
E[\rho] = T_s[\rho] + V_\mathrm{N}[\rho] + J_\mathrm{ee}[\rho] + E_\mathrm{xc}[\rho]
\end{displaymath}](img304.png) |
(38) |
Here, ![$T_s[\rho]$](img305.png) is the kinetic energy of non-interacting electrons,
is the kinetic energy of non-interacting electrons,
![$V_\mathrm{N}[\rho]$](img306.png) describes the electron-nuclei interaction and the so-called
Hartree term,
describes the electron-nuclei interaction and the so-called
Hartree term,
![$J_\mathrm{ee}[\rho]$](img307.png) , is the Coulombic interaction among the electrons:
, is the Coulombic interaction among the electrons:
The last term in equation 2.37 is the exchange
correlation energy functional
![$E_\mathrm{xc}[\rho]$](img314.png) which compensates for the
electron-electron interaction
which compensates for the
electron-electron interaction 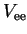 being described only by
the Coulomb interaction
being described only by
the Coulomb interaction 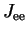 (thereby neglecting the exchange interaction
and the electron correlation interaction) and for the kinetic energy functional which
describes the kinetic energy for non-interacting electrons:
(thereby neglecting the exchange interaction
and the electron correlation interaction) and for the kinetic energy functional which
describes the kinetic energy for non-interacting electrons:
![\begin{displaymath}
E_\mathrm{xc}[\rho] = V_\mathrm{ee} - J_\mathrm{ee}[\rho] + T[\rho] - T_s[\rho]
\end{displaymath}](img317.png) |
(42) |
The exchange correlation energy functional also has to correct for a spurious
self interaction arising from 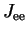 , which is in ab initio methods
canceled exactly by the exchange term, but in DFT actually is the largest
contribution to
, which is in ab initio methods
canceled exactly by the exchange term, but in DFT actually is the largest
contribution to
![$E_\mathrm{xc}[\rho]$](img314.png) .
.
The electronic ground-state density is found by minimizing the Kohn-Sham energy
functional, which is achieved by solving the Kohn-Sham equations:
![\begin{displaymath}
{\hat {\cal H}}^\mathrm{KS} \psi_i =
\left[ -\frac{\hbar^2}{...
...rho]}{\delta \rho({\bf r})} \right] \psi_i = \epsilon_i \psi_i
\end{displaymath}](img318.png) |
(43) |
Thus far, the DFT expressions are exact. However, an exact
expression for
![$E_\mathrm{xc}[\rho]$](img314.png) is not known, and one is forced to
use an approximate functional. Also, there is no straightforward way
in which the exchange correlation functional can be systematically
improved.
is not known, and one is forced to
use an approximate functional. Also, there is no straightforward way
in which the exchange correlation functional can be systematically
improved.
For an homogeneous electron gas or an electron gas with slow varying density,
one can show that
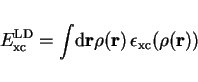 |
(44) |
The exchange correlation energy density function
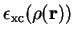 for the uniform electron gas is known to high accuracy from Monte Carlo calculations
of Ceperly and Alder[35]. Several parameterizations were used for this type
of functional, which are known as local density approximation (LDA) functionals.
Especially in solid-state physics, LDA works surprisingly well despite its
approximate nature. However, most chemical applications do not satisfy the
restriction of slowly varying electron density and the LDA fails. Much better
results are obtained by taking into account the density fluctuations, via the
gradient of the density. This has led to the development of various so-called
generalized gradient approximations (GGAs), of which the most popular is the
Becke[36] exchange functional:
for the uniform electron gas is known to high accuracy from Monte Carlo calculations
of Ceperly and Alder[35]. Several parameterizations were used for this type
of functional, which are known as local density approximation (LDA) functionals.
Especially in solid-state physics, LDA works surprisingly well despite its
approximate nature. However, most chemical applications do not satisfy the
restriction of slowly varying electron density and the LDA fails. Much better
results are obtained by taking into account the density fluctuations, via the
gradient of the density. This has led to the development of various so-called
generalized gradient approximations (GGAs), of which the most popular is the
Becke[36] exchange functional:
which has led to the acceptance of DFT as a valuable tool for computational
chemistry, after its introduction in 1988.
This functional contains one adjustable parameter 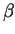 which was chosen so that
the sum of the LDA and Becke exchange terms accurately reproduce the exchange
energies of six noble gas atoms,
which was chosen so that
the sum of the LDA and Becke exchange terms accurately reproduce the exchange
energies of six noble gas atoms,  . A large number of other GGA
functionals for both correlation and exchange have been developed, of which the
most popular probably the 4 parameter LYP correlation functional[37] ,
the parameter-free Perdew86 correlation functional[38] and the Perdew91
exchange+correlation functional[39].
Throughout the present work, we will make use of Becke's exchange functional
and the Perdew86 correlation functional.
However, the search for the holy grail continues.
Routes to improvement are for example the mixing in of exact (Hartree-Fock)
exchange (so-called hybrid functionals, such as the B3LYP functional), the use of
highly parameterized GGA functionals which are fitted to large sets of empirical
molecular properties (e.g. the HCTH functional[40]), taking
the Laplacian of the density into account (e.g. the BLAP
functional[41]), correcting for the approximate kinetic energy
term[42], correction for the spurious Coulombic self interaction
(so-called SIC functionals[43]) and imposing of the correct asymptotic
behavior (e.g. the VanLeeuwen-Baerends functional[44]).
Other important progress, which makes DFT particularly popular by chemists,
is made in the development of computer programs that calculate chemical and
physical properties, such as spectroscopic observables, a posteriori,
using the Kohn-Sham density. The reader interested in the technical details
of density functional theory and its application in chemistry
might wish to read references BeGr97,DFT,DFT2,BiBa00.
. A large number of other GGA
functionals for both correlation and exchange have been developed, of which the
most popular probably the 4 parameter LYP correlation functional[37] ,
the parameter-free Perdew86 correlation functional[38] and the Perdew91
exchange+correlation functional[39].
Throughout the present work, we will make use of Becke's exchange functional
and the Perdew86 correlation functional.
However, the search for the holy grail continues.
Routes to improvement are for example the mixing in of exact (Hartree-Fock)
exchange (so-called hybrid functionals, such as the B3LYP functional), the use of
highly parameterized GGA functionals which are fitted to large sets of empirical
molecular properties (e.g. the HCTH functional[40]), taking
the Laplacian of the density into account (e.g. the BLAP
functional[41]), correcting for the approximate kinetic energy
term[42], correction for the spurious Coulombic self interaction
(so-called SIC functionals[43]) and imposing of the correct asymptotic
behavior (e.g. the VanLeeuwen-Baerends functional[44]).
Other important progress, which makes DFT particularly popular by chemists,
is made in the development of computer programs that calculate chemical and
physical properties, such as spectroscopic observables, a posteriori,
using the Kohn-Sham density. The reader interested in the technical details
of density functional theory and its application in chemistry
might wish to read references BeGr97,DFT,DFT2,BiBa00.



Next: Solvation effects on the
Up: Techniques
Previous: Car-Parrinello molecular dynamics
Contents
Bernd Ensing
2003-06-13
![]() , or to minimize the atomic potential energy by
optimizing the atomic degrees of freedom, the positions
, or to minimize the atomic potential energy by
optimizing the atomic degrees of freedom, the positions
![]() .
But we have not yet introduced the quantum mechanical relation between
the energy and the electronic coefficients and atomic positions,
to obtain the forces on the atoms and coefficients (eq. 2.30).
The reason is, that in principle various quantum mechanical (or even
semi-empirical methods) can be used, such as the Hartree-Fock method
or the configurational interaction method. Hartree-Fock, however, lacks
for many practical systems the desired chemical accuracy while on the
other hand the configurational interaction method, although it can be highly
accurate, is unpractical due to its dramatic scaling of the computational
expense with the number of electrons.
In practice, therefore, the energy and the forces are obtained
from an electronic structure calculation using density functional
theory (DFT), which is both accurate and has a favorable scaling.
.
But we have not yet introduced the quantum mechanical relation between
the energy and the electronic coefficients and atomic positions,
to obtain the forces on the atoms and coefficients (eq. 2.30).
The reason is, that in principle various quantum mechanical (or even
semi-empirical methods) can be used, such as the Hartree-Fock method
or the configurational interaction method. Hartree-Fock, however, lacks
for many practical systems the desired chemical accuracy while on the
other hand the configurational interaction method, although it can be highly
accurate, is unpractical due to its dramatic scaling of the computational
expense with the number of electrons.
In practice, therefore, the energy and the forces are obtained
from an electronic structure calculation using density functional
theory (DFT), which is both accurate and has a favorable scaling.
![]() .
In other words, the density is uniquely determined given a potential,
and vice versa. All properties are therefore a functional of the
density, because the density determines the potential, which
determines the Hamiltonian, which determines the energy
(
.
In other words, the density is uniquely determined given a potential,
and vice versa. All properties are therefore a functional of the
density, because the density determines the potential, which
determines the Hamiltonian, which determines the energy
(![]() ) and the wave function (
) and the wave function (![]() ), from which
all physical properties can be determined. This theorem was proven
in 1964 by Hohenberg and Kohn, using the variational principle
for systems with a non-degenerate ground-state. Hohenberg and Kohn
also showed that for a given potential
), from which
all physical properties can be determined. This theorem was proven
in 1964 by Hohenberg and Kohn, using the variational principle
for systems with a non-degenerate ground-state. Hohenberg and Kohn
also showed that for a given potential ![]() , which corresponds
with a ground-state
, which corresponds
with a ground-state ![]() and ground-state energy
and ground-state energy ![]() ,
the energy functional
,
the energy functional ![]() has its minimum equal to
has its minimum equal to ![]() at the ground-state density (second Hohenberg-Kohn theorem), or:
at the ground-state density (second Hohenberg-Kohn theorem), or:
![\begin{displaymath}
\left< \Psi[\rho] \left \vert {\hat {\cal H}} \right\vert \P...
...r}) + T[\rho] + V_\mathrm{ee}[\rho] =
E_v[\rho] \ge E_0[\rho]
\end{displaymath}](img297.png)
![]() -electron density
was given by Kohn and Sham in a one-electron formalism, posing
that there exists an auxiliary system of
-electron density
was given by Kohn and Sham in a one-electron formalism, posing
that there exists an auxiliary system of ![]() non-interacting
electrons, feeling only a local potential
non-interacting
electrons, feeling only a local potential ![]() which
yields exactly the same density as the system of interacting
electrons with potential
which
yields exactly the same density as the system of interacting
electrons with potential ![]() . The electron density is
represented by the sum of the densities of the
. The electron density is
represented by the sum of the densities of the ![]() doubly occupied
single-particle spatial orbitals,
doubly occupied
single-particle spatial orbitals,
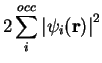
![]() is the kinetic energy of non-interacting electrons,
is the kinetic energy of non-interacting electrons,
![]() describes the electron-nuclei interaction and the so-called
Hartree term,
describes the electron-nuclei interaction and the so-called
Hartree term,
![]() , is the Coulombic interaction among the electrons:
, is the Coulombic interaction among the electrons:
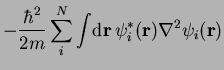
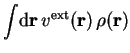
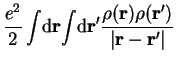
![\begin{displaymath}
E_\mathrm{xc}[\rho] = V_\mathrm{ee} - J_\mathrm{ee}[\rho] + T[\rho] - T_s[\rho]
\end{displaymath}](img317.png)
![\begin{displaymath}
{\hat {\cal H}}^\mathrm{KS} \psi_i =
\left[ -\frac{\hbar^2}{...
...rho]}{\delta \rho({\bf r})} \right] \psi_i = \epsilon_i \psi_i
\end{displaymath}](img318.png)