One of the proposed second reaction steps in the oxidation catalysis by the Fenton-like reagent involves homolysis of the oxygen-oxygen bond of the iron(III)hydro-peroxo species, producing an OH. radical and the ferryl ion (reaction 6.5). We have studied this reaction in detail, since it has emerged from our static DFT calculations as one of the most likely second reaction steps, in particular when the hydrolysis of a water ligand is simultaneously taken into account.
We have performed constrained AIMD simulations to calculate the
free energy profile for the oxygen-oxygen bond homolysis reaction
of the [Fe![]() (H
(H![]() O)
O)![]() OOH]
OOH]![]() complex into
an iron(IV)oxo species and an OH. radical in water. The oxygen-oxygen
bond length
complex into
an iron(IV)oxo species and an OH. radical in water. The oxygen-oxygen
bond length ![]() was taken as the constrained reaction coordinate,
which seems intuitively a good choice that includes the most important
contribution to the intrinsic reaction coordinate. The main drawback of
this choice is however that it does not prevent unwanted side reactions
such as the abstraction of solvent molecule hydrogens by the OH.
radical produced. For large values of the constrained
reaction coordinate
was taken as the constrained reaction coordinate,
which seems intuitively a good choice that includes the most important
contribution to the intrinsic reaction coordinate. The main drawback of
this choice is however that it does not prevent unwanted side reactions
such as the abstraction of solvent molecule hydrogens by the OH.
radical produced. For large values of the constrained
reaction coordinate ![]() , the OH. radical can abstract a
solvent hydrogen forming H
, the OH. radical can abstract a
solvent hydrogen forming H![]() O, while an OH. species "jumps" through
the solvent by a chain reaction. The sampled force
of constraint, associated with the force necessary to keep a H
O, while an OH. species "jumps" through
the solvent by a chain reaction. The sampled force
of constraint, associated with the force necessary to keep a H![]() O
molecule (instead of the OH.) constrained to the oxygen of the
iron complex, will then be of course meaningless.
We will therefore take the same approach as was done in the work by Trout and
Parrinello, who studied the dissociation of H
O
molecule (instead of the OH.) constrained to the oxygen of the
iron complex, will then be of course meaningless.
We will therefore take the same approach as was done in the work by Trout and
Parrinello, who studied the dissociation of H![]() O in water in H
O in water in H![]() and
OH
and
OH![]() with the
same technique,[207] and only calculated the profile up to
(or at least very close to) the transition state. Since the subsequent
reaction of the OH. "jumping" into the solvent is thermoneutral, the free energy
profile of the homolysis is not expected to decrease by more than a few kcal/mol
beyond the transition state (due to the increasing entropy of the leaving
OH. radical and the solvation of the oxo site).
Moreover, the transition state energy is the more important parameter
to determine whether the oxygen-oxygen homolysis is indeed a probable mechanism.
with the
same technique,[207] and only calculated the profile up to
(or at least very close to) the transition state. Since the subsequent
reaction of the OH. "jumping" into the solvent is thermoneutral, the free energy
profile of the homolysis is not expected to decrease by more than a few kcal/mol
beyond the transition state (due to the increasing entropy of the leaving
OH. radical and the solvation of the oxo site).
Moreover, the transition state energy is the more important parameter
to determine whether the oxygen-oxygen homolysis is indeed a probable mechanism.
|
Eight constrained AIMD runs were performed with constrained oxygen-oxygen bond
lengths varying from
![]() Å.
The initial configuration of each constrained simulation was taken from
the last frame of the first simulation of hydroperoxo iron(III)
in water, including the hydronium ion (see section 6.3.2).
For each system, a short AIMD simulation was started to bring
Å.
The initial configuration of each constrained simulation was taken from
the last frame of the first simulation of hydroperoxo iron(III)
in water, including the hydronium ion (see section 6.3.2).
For each system, a short AIMD simulation was started to bring ![]() to
the desired value in 2000 steps. Then equilibration of each system took place
for 2 picoseconds, after which the force of constraint was accumulated for
another 2 picoseconds. The obtained values for the mean force of constraint
are denoted by crosses and circles in
figure 6.4 and fitted with a quadratic spline.
Integration of the mean force of constraint gives the Helmholtz free energy profile
to
the desired value in 2000 steps. Then equilibration of each system took place
for 2 picoseconds, after which the force of constraint was accumulated for
another 2 picoseconds. The obtained values for the mean force of constraint
are denoted by crosses and circles in
figure 6.4 and fitted with a quadratic spline.
Integration of the mean force of constraint gives the Helmholtz free energy profile
![]() , where we take the minimum at
, where we take the minimum at ![]() Å
for the offset of the energy scale (solid line). The circles indicate those constrained
simulations during which the O
Å
for the offset of the energy scale (solid line). The circles indicate those constrained
simulations during which the O![]() H. radical abstracts a hydrogen and
transforms into a water molecule. Indeed, this occurs for the
H. radical abstracts a hydrogen and
transforms into a water molecule. Indeed, this occurs for the
![]() values close to the transition state, for which the
O
values close to the transition state, for which the
O![]() H part has acquired enough radical character to abstract a hydrogen
when a nearby solvent molecule moves into a suitable position.
In both cases (at
H part has acquired enough radical character to abstract a hydrogen
when a nearby solvent molecule moves into a suitable position.
In both cases (at
![]() Å and at
Å and at
![]() Å),
the hydrogen abstraction occurs after about 1.3 ps simulation. The values for
the mean force of constraint denoted by the circles are the averages
over these 1.3 ps. After the H abstraction by O
Å),
the hydrogen abstraction occurs after about 1.3 ps simulation. The values for
the mean force of constraint denoted by the circles are the averages
over these 1.3 ps. After the H abstraction by O![]() H., the force of
constraint goes to zero, or becomes even slightly positive (repulsive)
because the produced water molecule is repelled by the oxo ligand at
the short constrained oxygen-oxygen distance, rather than attracted like
the OH. radical shortly before. For the O-O distance of
H., the force of
constraint goes to zero, or becomes even slightly positive (repulsive)
because the produced water molecule is repelled by the oxo ligand at
the short constrained oxygen-oxygen distance, rather than attracted like
the OH. radical shortly before. For the O-O distance of
![]() Å, the average force of constraint (over
the 1.3 ps before the H abstraction) is almost equal to zero,
which indicates that this O-O distance is indeed very close to the
transition state.
Å, the average force of constraint (over
the 1.3 ps before the H abstraction) is almost equal to zero,
which indicates that this O-O distance is indeed very close to the
transition state.
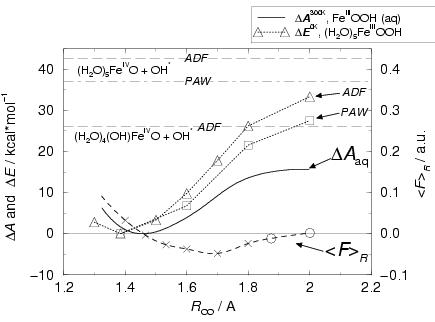
The free energy reaction barrier for the homolysis reaction in water
is found to be
![]() kcal/mol, which is low compared
to the
kcal/mol, which is low compared
to the ![]() kcal/mol (ground-state) energy change found
for the reaction in vacuo, or even the
kcal/mol (ground-state) energy change found
for the reaction in vacuo, or even the ![]() kcal/mol
for the hydrolyzed complexes in vacuo (reaction I in
table 6.1). We have also plotted twice the contour for the
reaction energy
kcal/mol
for the hydrolyzed complexes in vacuo (reaction I in
table 6.1). We have also plotted twice the contour for the
reaction energy
![]() of the homolysis of the
[Fe
of the homolysis of the
[Fe![]() (H
(H![]() O)
O)![]() OOH]
OOH]![]() complex in vacuo (triangles
connected by a dotted line, and the value for infinite product separation
indicated by the vertical dashed line); once computed with the ADF program
and once computed with the PAW program. Unfortunately, we find an
increasing underestimation of the energy profile with increasing
complex in vacuo (triangles
connected by a dotted line, and the value for infinite product separation
indicated by the vertical dashed line); once computed with the ADF program
and once computed with the PAW program. Unfortunately, we find an
increasing underestimation of the energy profile with increasing ![]() ,
calculated with PAW compared to the highly accurate (all-electron, large
basis set) ADF results, with a maximum difference of 5.6 kcal/mol
at
,
calculated with PAW compared to the highly accurate (all-electron, large
basis set) ADF results, with a maximum difference of 5.6 kcal/mol
at
![]() Å and at infinite separation. The error does not
seem to be due to the plane-wave cutoff of 30 Ry (it is only reduced by
0.5 kcal/mol when going to 50 Ry) and can be attributed to the partial
waves for the inner region of the valence electrons and the projector
functions for the iron atom used in the PAW calculations.
Although bond energies in iron(III) and iron(IV) complexes
computed with PAW agree within 2 kcal/mol with those using ADF, we
have found after extensive tests that the stability of the (formally)
Fe
Å and at infinite separation. The error does not
seem to be due to the plane-wave cutoff of 30 Ry (it is only reduced by
0.5 kcal/mol when going to 50 Ry) and can be attributed to the partial
waves for the inner region of the valence electrons and the projector
functions for the iron atom used in the PAW calculations.
Although bond energies in iron(III) and iron(IV) complexes
computed with PAW agree within 2 kcal/mol with those using ADF, we
have found after extensive tests that the stability of the (formally)
Fe![]() configuration is overestimated by 5-6 kcal/mol with respect
to the (formally) Fe
configuration is overestimated by 5-6 kcal/mol with respect
to the (formally) Fe![]() configuration.
This indicates that also the free energy barrier of the homolysis
in aqueous solution has to be corrected for this error so that
the true value becomes
configuration.
This indicates that also the free energy barrier of the homolysis
in aqueous solution has to be corrected for this error so that
the true value becomes
![]() kcal/mol.
Solvent effects thus strongly reduce the transition state barrier
for the O-O homolysis reaction in water. The main contribution to this
effect is expected to originate from the larger absolute energy of solvation
for the separating transition state complex (Fe
kcal/mol.
Solvent effects thus strongly reduce the transition state barrier
for the O-O homolysis reaction in water. The main contribution to this
effect is expected to originate from the larger absolute energy of solvation
for the separating transition state complex (Fe![]() =O
=O![]() OH.)
in comparison with the reactant molecule, Fe
OH.)
in comparison with the reactant molecule, Fe![]() OOH.
(Note that often reaction barriers are increased in aqueous solution,
because the sum of the absolute energies of solvation for two reacting
molecules is typically larger than that for the single transition state
complex.)
OOH.
(Note that often reaction barriers are increased in aqueous solution,
because the sum of the absolute energies of solvation for two reacting
molecules is typically larger than that for the single transition state
complex.)
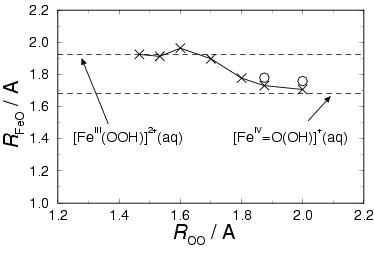
The upper graph in figure 6.5 illustrates the
transformation of the Fe![]() -OOH
-OOH![]() bond into an
Fe
bond into an
Fe![]() =O
=O![]() bond by showing the average
Fe-O
bond by showing the average
Fe-O![]() distance as a function of the reaction coordinate.
The two dashed lines indicate the average
distance as a function of the reaction coordinate.
The two dashed lines indicate the average ![]() for the
pentaaquairon(III)hydroperoxo complex in water (obtained from the
first 5 ps simulation described in section 6.3.2),
equal to 1.922 Å and the average
for the
pentaaquairon(III)hydroperoxo complex in water (obtained from the
first 5 ps simulation described in section 6.3.2),
equal to 1.922 Å and the average ![]() for the
ferryl ion in water equal to 1.680 Å. This latter number was
obtained from the [Fe
for the
ferryl ion in water equal to 1.680 Å. This latter number was
obtained from the [Fe![]() O(OH)]
O(OH)]![]() moiety produced in the
reaction between Fe
moiety produced in the
reaction between Fe![]() and H
and H![]() O
O![]() in water (cf.
ref bernd4), in which indeed a water ligand hydrolyzed to
form the OH
in water (cf.
ref bernd4), in which indeed a water ligand hydrolyzed to
form the OH![]() ligand as suggested in section 6.3.1.
This apparent increased acidity of the iron(IV) species compared
to that of iron(III) is discussed below.
Proceeding with the Fe-O distance, we see that
ligand as suggested in section 6.3.1.
This apparent increased acidity of the iron(IV) species compared
to that of iron(III) is discussed below.
Proceeding with the Fe-O distance, we see that ![]() decreases rapidly when the oxygen-oxygen separation becomes
larger than 1.7 Å, which indicates the changing character of the
metal and the bonds. At the reaction coordinate value of
decreases rapidly when the oxygen-oxygen separation becomes
larger than 1.7 Å, which indicates the changing character of the
metal and the bonds. At the reaction coordinate value of
![]() Å, the average
Å, the average ![]() (over the 1.3 ps simulation
before the O
(over the 1.3 ps simulation
before the O![]() H. radical abstracts a solvent hydrogen) has decreased
practically to the average value of free [Fe
H. radical abstracts a solvent hydrogen) has decreased
practically to the average value of free [Fe![]() O(OH)]
O(OH)]![]() ,
which indicates that at
,
which indicates that at
![]() Å the reaction is close
to completion. The open circles in figure 6.5 denote
the averages over the simulation part after the O
Å the reaction is close
to completion. The open circles in figure 6.5 denote
the averages over the simulation part after the O![]() H. radical
transformed into H
H. radical
transformed into H![]() O
O![]() by H-abstraction from an adjacent solvent
molecule. At
by H-abstraction from an adjacent solvent
molecule. At
![]() Å, the average
Å, the average ![]() is a little
larger than expected from the trend. This is the result of proton donation
from the iron complex (i.e. hydrolysis) to the aqueous solvent
during the constrained simulation at this reaction coordinate value,
which we will explain below.
is a little
larger than expected from the trend. This is the result of proton donation
from the iron complex (i.e. hydrolysis) to the aqueous solvent
during the constrained simulation at this reaction coordinate value,
which we will explain below.
|
As mentioned before, we expect hydrolysis of water ligands to lower
the reaction energy of the oxygen-oxygen homolysis (see the change from
42.6 to 26.1 kcal/mol for reaction I in table 6.1), and secondly
we expect hydrolysis to become more frequent for iron(IV) (product)
compared to iron(III) (reactant). In our short constrained dynamics
simulations of the enforced O![]() -O
-O![]() homolysis in aqueous
solution, we can
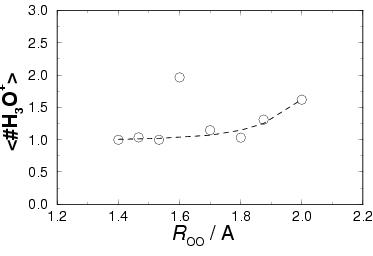
indeed observe these trends by plotting the average number of
hydronium ions in the solvent versus the reaction coordinate
homolysis in aqueous
solution, we can
indeed observe these trends by plotting the average number of
hydronium ions in the solvent versus the reaction coordinate ![]() (see circles in the lower graph in figure 6.5
and the dotted lines to guide the eye). The water ligand O-H distances
(see circles in the lower graph in figure 6.5
and the dotted lines to guide the eye). The water ligand O-H distances
![]() were taken as the order parameters: all
10
were taken as the order parameters: all
10
![]() Å means that no hydrolysis has taken place.
At the reactant side (small
Å means that no hydrolysis has taken place.
At the reactant side (small ![]() ),
hydrolysis is rarely observed during the 2 ps simulations and only
the one hydronium ion which we started with (originating from the
hydrogen peroxide when it reacted with iron(III), see previous sections)
brings the average number to 1 H
),
hydrolysis is rarely observed during the 2 ps simulations and only
the one hydronium ion which we started with (originating from the
hydrogen peroxide when it reacted with iron(III), see previous sections)
brings the average number to 1 H![]() O
O![]() . Going towards higher
. Going towards higher
![]() values, the oxidation state of the iron ion goes
to four and the complex is seen to become more acidic, confirming the
second trend mentioned. At
values, the oxidation state of the iron ion goes
to four and the complex is seen to become more acidic, confirming the
second trend mentioned. At
![]() Å,
62 % of the time a (second) proton was donated to the solvent by the complex
(in the 1.3 ps before H abstraction by the leaving O
Å,
62 % of the time a (second) proton was donated to the solvent by the complex
(in the 1.3 ps before H abstraction by the leaving O![]() H.
from a solvent water), which justifies the previous comparison of
H.
from a solvent water), which justifies the previous comparison of ![]() with that of the hydrolyzed ferryl ion ([Fe
with that of the hydrolyzed ferryl ion ([Fe![]() O(OH)]
O(OH)]![]() )
in the upper graph.
At
)
in the upper graph.
At
![]() Å, the average number of 1.96 hydronium ions seems out
of order in this trend. In the simulations, we see that for this run the
two hydronium ions are most of the time jumping freely around in the
solvent. In the other runs however, we find that most of the time
one of the protons jumps back and forth between the ligand and a solvent
water molecule and thus remains in the neighborhood of the complex.
Apparently we can separate the ligand hydrolysis into two stages which
show resemblance with the dynamics of free hydronium ion transfer
in water (cf. ref. TLSP2), namely:
1) a fast process which involves the sharing of the proton
by a ligand and a solvent molecule (or two solvent waters for the
free hydronium ion, with a frequency
Å, the average number of 1.96 hydronium ions seems out
of order in this trend. In the simulations, we see that for this run the
two hydronium ions are most of the time jumping freely around in the
solvent. In the other runs however, we find that most of the time
one of the protons jumps back and forth between the ligand and a solvent
water molecule and thus remains in the neighborhood of the complex.
Apparently we can separate the ligand hydrolysis into two stages which
show resemblance with the dynamics of free hydronium ion transfer
in water (cf. ref. TLSP2), namely:
1) a fast process which involves the sharing of the proton
by a ligand and a solvent molecule (or two solvent waters for the
free hydronium ion, with a frequency ![]() 5 ps
5 ps![]() )
and 2) a much slower process, which is connected to
the actual stepwise diffusion of the hydronium ion through the solvent.
The latter process concerns changes in the second coordination
shell hydrogen bond
network which in water was found to have a frequency of about
0.5 ps
)
and 2) a much slower process, which is connected to
the actual stepwise diffusion of the hydronium ion through the solvent.
The latter process concerns changes in the second coordination
shell hydrogen bond
network which in water was found to have a frequency of about
0.5 ps![]() .[53] Obviously, our 2 ps AIMD simulations are
too short to capture good statistics of the slow process, so that
in each simulation we either see the excess proton being shared
by two water molecules in the solvent (namely in the run with
.[53] Obviously, our 2 ps AIMD simulations are
too short to capture good statistics of the slow process, so that
in each simulation we either see the excess proton being shared
by two water molecules in the solvent (namely in the run with
![]() Å,) or it is being shared by a ligand and a
solvent molecule (as in all other runs). Fortunately, already from the
distribution in the fast jumping process we obtain information
on the acidity (i.e. the ability to donate a proton to
the aqueous environment) of the iron complex, as shown in figure
6.5, but for comparison with experimental p
Å,) or it is being shared by a ligand and a
solvent molecule (as in all other runs). Fortunately, already from the
distribution in the fast jumping process we obtain information
on the acidity (i.e. the ability to donate a proton to
the aqueous environment) of the iron complex, as shown in figure
6.5, but for comparison with experimental p![]() values we need to include also the slower hydronium ion transport.
The run with
values we need to include also the slower hydronium ion transport.
The run with
![]() Å confirms the first trend
mentioned in this paragraph: replacement of a water ligand
by a hydroxo ligand facilitates the oxygen-oxygen homolysis. In
our constrained MD exercise this is seen by the lower absolute constraint
force resulting in a dent in the mean constraint force profile in
figure 6.4 and also in the
Å confirms the first trend
mentioned in this paragraph: replacement of a water ligand
by a hydroxo ligand facilitates the oxygen-oxygen homolysis. In
our constrained MD exercise this is seen by the lower absolute constraint
force resulting in a dent in the mean constraint force profile in
figure 6.4 and also in the ![]() profile in figure 6.5. If we could afford
better statistics by performing much longer simulations,
in principle the two states (pentaaqua versus hydrolyzed tetraaqua
hydroxo complex) would be sampled with correct weights, giving the
correct mean force of constraint and free energy profile. In our
result however, we find for all runs except the one with
profile in figure 6.5. If we could afford
better statistics by performing much longer simulations,
in principle the two states (pentaaqua versus hydrolyzed tetraaqua
hydroxo complex) would be sampled with correct weights, giving the
correct mean force of constraint and free energy profile. In our
result however, we find for all runs except the one with
![]() Å
mostly the pentaaqua complex, so that we should take into account an
overestimation of a few kcal/mol for the free energy barrier.
Moreover, if we would be interested in calculating the reaction
rate of the O-O homolysis reaction in water we should either control the
hydrolysis process by including it in the reaction coordinate or
we should expect a large deviation from the transition state theory
reaction rate, and therefore perform the cumbersome computation
of the transmission coefficient in the pre-exponential factor.
We can nevertheless conclude that our estimation of the free energy
barrier of the O-O homolysis of the iron(III)hydroperoxo intermediate
in aqueous solution indicates that this formation of a ferryl ion
and the OH. radical is a likely second step in Fenton-like chemistry.
And secondly, the simulations confirm the hypothesis that water ligand
hydrolysis plays an important role in the process.
Å
mostly the pentaaqua complex, so that we should take into account an
overestimation of a few kcal/mol for the free energy barrier.
Moreover, if we would be interested in calculating the reaction
rate of the O-O homolysis reaction in water we should either control the
hydrolysis process by including it in the reaction coordinate or
we should expect a large deviation from the transition state theory
reaction rate, and therefore perform the cumbersome computation
of the transmission coefficient in the pre-exponential factor.
We can nevertheless conclude that our estimation of the free energy
barrier of the O-O homolysis of the iron(III)hydroperoxo intermediate
in aqueous solution indicates that this formation of a ferryl ion
and the OH. radical is a likely second step in Fenton-like chemistry.
And secondly, the simulations confirm the hypothesis that water ligand
hydrolysis plays an important role in the process.