The first reaction step in Fenton-like chemistry in water: formation and characterization of the iron(III) hydroperoxo species

a) Formation. In this section, we will describe the results of our study of the most likely intermediate formed in a mixture of iron(III) ions and hydrogen peroxide in water. We will follow the same approach as in our previous work[146] on the active intermediate formed from iron(II) and hydrogen peroxide, which makes it easy to compare the reactions with each other. In this previous work on Fenton's reagent, we showed two illustrative pathways of the reaction between Fe $^{2+}$ and H

in water producing the high-valent iron-oxo species [Fe $^{\rm {IV}}$ O] $^{2+}$ . The ferryl ion formation occurred either in two steps, via an iron(IV) dihydroxo intermediate ([Fe $^{\rm {IV}}$ (OH)

] $^{2+}$ ), if we started from a [Fe $^{\rm {II}}$ (H

)] $^{2+}$ complex, or via a more direct ``rebound'' mechanism if we started from separated Fe $^{2+}$ and H

, thus including the coordination process of H

to an empty iron(II) site. The [Fe $^{\rm {II}}$ (H

)] $^{2+}$ complex was not found to be a stable intermediate in aqueous solution, unlike [(H

Fe $^{\rm {II}}$ (H

)] $^{2+}$ in vacuo.

For the present reaction of hydrogen peroxide with iron(III), we performed a Car-Parrinello MD simulation of H

coordinated to Fe $^{3+}$ , surrounded by 31 water molecules in a cubic box with periodic boundary conditions. We used a snapshot from the study of the [Fe $^{\rm {II}}$ (H

)] $^{2+}$ complex in water for the initial configuration, and removed in that configuration one spin-down electron from the system. The total spin was thus

, and the total charge equaled 3+, which was counterbalanced by a uniformly distributed 3- charge. We relaxed the system to the new situation, by an MD run of 3.5 ps. During this time of equilibration, bond constraints were applied to the Fe-O and O-O bonds, fixing these bond lengths to their equilibrium distances, in order to prevent a premature breakup of the complex by the unrelaxed environment. Next, we removed the constraints and followed the evolution of the [Fe $^{\rm {III}}$ (H

)] $^{3+}$ complex in water for 5 ps.

Already in the equilibration phase, hydrolysis had taken place on the $\alpha$ -oxygen of the ligated hydrogen peroxide ( $\alpha$ denotes the oxygen connected to iron), donating the proton to the water solvent:

Our simulation thus started with an iron(III)hydroperoxo complex and a hydronium ion in water, and no further spontaneous transformation took place during the 5 ps of molecular dynamics. The oxygen-oxygen bond did not break but instead fluctuated around an average bond length of $R_{\rm {OO}}=1.466$ Å, contrary to the oxygen-oxygen bond of hydrogen peroxide coordinated to iron(II) which was found to cleave spontaneously in aqueous solution. Also was the aqueous proton not seen to jump back on the hydroperoxo ligand during our simulation, as with the dynamic equilibria we have for instance seen for hydrolysis of aqua ligands of hexaaquairon(III) (see before) and the [(H

Fe $^{\rm {IV}}$ (OH)

] $^{2+}$ complex.[171] The OH bond length fluctuations of the aqua ligands were significantly larger than the ones in hexaaquairon(II), with maxima of $R_{\rm {OH}}^{\rm {max}}=1.4$ Å ( $R_{\rm {OH}}^{\rm {max}}=1.1$ Å in hexaaquairon(II)), almost donating a proton to the solvent, but never dissociating completely. This indicates that the acidity of [(H

Fe $^{\rm {III}}$ (OOH)] $^{2+}$ is in between that of hexaaquairon(II) and hexaaquairon(III).

To make sure that the hydroperoxo ligand formation (during the equilibration phase) was not the result of non-equilibrium solvent effects, we started a second MD simulation from a configuration of the equilibration phase at a time just before the hydrogen peroxide hydrolysis took place. This time, we constrained the O $^\alpha$ -H bond length to prevent hydrolysis during a 1.2 ps equilibration run, after which we removed the constraint and again followed the evolution of the system. Although during most of the equilibration time now an aqua ligand donated a proton to the solvent (reaction equation 6.8),

this proton is united with the hydroxo ligand again at the end of the equilibration so that indeed we started with a [(H

Fe $^{\rm {III}}$ (H

)] $^{3+}$ complex in water. After 0.2 ps, again hydrolysis of the coordinated hydrogen peroxide takes place so that the Fe $^{\rm {III}}$ OOH moiety is formed which again remains stable for the next 1.75 ps, after which we stopped the computation. Clearly, this second simulation shows that the H

ligand hydrolysis was not an effect of the unrelaxed environment (which was not clear from the first simulation). And secondly, the higher stability of the O-O bond compared to the iron(II)hydrogen-peroxide case is not a result of the H

hydrolysis, since no O-O lysis occurred spontaneously when only the O $^\alpha$ -H bond length was constrained.

Finally, we performed a last AIMD simulation in which we also wanted to include the formation of a coordination bond of hydrogen peroxide to a vacant coordination site of iron(III). Starting with a random configuration in which the solvated reactants are separated from each other a certain distance is however very unpractical, because the probability of a spontaneous coordination is too small to make an observation likely in the relatively short time of a typical AIMD simulation. We therefore applied a simple device, which had worked already very well for the iron(II)/H

system.[146] We carried out a constrained AIMD simulation of hydrogen peroxide coordinated to iron(III) in water. The O-O bond, the Fe-O $^\alpha$ bond and the O $^\alpha$ -H bond were fixed to their equilibrium distances and also a bond constraint was applied to the distance between the peroxide's O $^\beta$ and the hydrogen of an adjacent water ligand, fixing this distance to $R_{\rm {OH}}=2.0$ Å. The small strain induced in the five-membered ring which is closed by the $R_{\rm {OH}}$ constraint (see also figure 6.1) was enough to pull hydrogen peroxide from the aquairon complex when we released all constraints, except the O $^\alpha$ -H bond constraint. This process is illustrated in figure 6.2, showing the distances Fe-O $^\alpha$ , Fe-O $^\beta$ , O $^\alpha$ -O $^\beta$ and O $^\alpha$ -H as a function of time, starting just before the moment we released these bond constraints.

**Figure 6.2:** The Fe-O $^\alpha$ , Fe-O $^\beta$ , O $^\alpha$ -O $^\beta$ and O $^\alpha$ -H distances as a function of time during the AIMD simulation of HO and Fe $^{3+}$ in water, starting from the last part of the equilibration phase (coordinated Fe-HO complex). After ps, Fe-O $^\alpha$ increases as HO leaves the coordination shell. At a separation of more than 3 Å, all velocities are reversed and simulation shows the process of coordination of hydrogen peroxide occurring almost simultaneous with the hydrolysis forming the iron(III)hydroperoxo moiety.

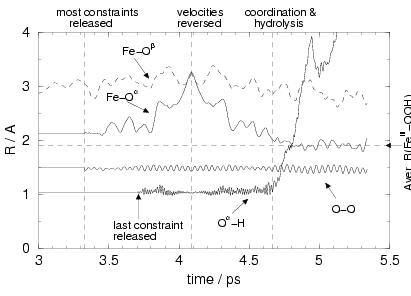
After release of all constraints except the O $^\alpha$ -H bond constraint, at

ps, the Fe-O $^\alpha$ bond starts to break, which is visible in figure 6.2 as the appearance of oscillations with increasing amplitude of $R_{{\rm Fe-O}^\alpha}$ , and at

ps, Fe and O $^\alpha$ clearly separate. During the dissociation process, at

ps, we also released the O $^\alpha$ H bond constraint. At time $t\approx4.1$ ps, we now have a situation where the Fe-O $^\alpha$ distance has increased to more than 3 Å i.e. the iron aqua complex and H

are separated from each other by at least 3 Å, with velocities that will lead to further separation. At this point, we reverse all the velocities (including those of the electronic wave function degrees of freedom and the Nosé thermostat variable) so that the reactants will now approach each other in the same way as they separated. The difference of course is that the O $^\alpha$ -H is now free to dissociate. In figure 6.2, we indeed see that as soon as hydrogen peroxide coordinates to the Fe $^{3+}$ ion, the O $^\alpha$ -H bond breaks, the proton moves into the solvent and the iron(III)hydroperoxo complex is being formed.

These illustrative pathways, confirm our inference from the calculation in vacuum (table 6.1), that formation of the Fe(III)(OOH) species is a likely candidate for the initial step in the Fenton-like reaction, in agreement with experiment, and secondly, that the oxygen-oxygen bond does not break so easily as in hydrogen peroxide coordinated to iron(II), which ultimately led to the ferryl ion as the most likely active intermediate in the Fe(II) catalysis. Moreover, formation of [Fe $^{\rm {III}}$ (H

(OOH)] $^{2+}$ seems much more likely than formation of [Fe $^{\rm {III}}$ (H

(OH)(H

)] $^{2+}$ , in agreement with table 6.1. This implies that as the second step of the Fenton-like reaction we should investigate the subsequent transformation of Fe(III)(OOH). This will be done in subsection 6.3.3. However, we will first investigate further the iron(III)hydroperoxo complex itself, making a connection with the experimental characterization of this moiety by vibrational spectroscopy of this metal-ligand system in various solvents and with different ligand environments.

b) Characterization: Fe(III)-OOH vibrations. Spectroscopic experiments have indicated that the spin-state of Fe(III)OOH complexes has a strong effect on the Fe-O and the O-O bond strengths[199,200]. Resonance Raman spectroscopy on low-spin iron(III)hydroperoxo complexes with large ligands such as N4Py (

-bis-(2-pyridylmethyl)-

-bis(2-pyridyl)methylamine)[201], TPA (tris-(2-pyridylmethyl)-amine)[200] and TPEN (

'-tetrakis-(2-pyridylmethyl)-ethane-1,2-diamine)[202] show O-O vibrations with frequencies between 789-801 cm $^{-1}$ and Fe-O vibrations between 617-632 cm $^{-1}$ . High-spin complexes show stronger O-O bonds ( $\nu_{\rm {O-O}}$

844 cm $^{-1}$ ) and weaker Fe-O bonds ( $\nu_{\rm {Fe-O}}$

503 cm $^{-1}$ ). The spin-state is normally dictated by the ligand field splitting 10

caused by the ligands, but in our computer experiments we can simply fix the number of spin-up and spin-down electrons. We have thus calculated the Fe(III)OOH frequencies of the complex in water at

K for both spin states. This was done by performing an AIMD simulation for each spin-state starting from the last frame of the first simulation of Fe(III)OOH (see previous section). The hydronium ion in the solvent was replaced with a water molecule to avoid the influence it could have on the vibrations of the complex. We calculated a 2.5 ps AIMD trajectory, from which the last 1.5 ps was used to calculate the velocity autocorrelation of specific vibrations, such as the oxygen-oxygen bond stretching $d_{\rm OO}(t)$ . 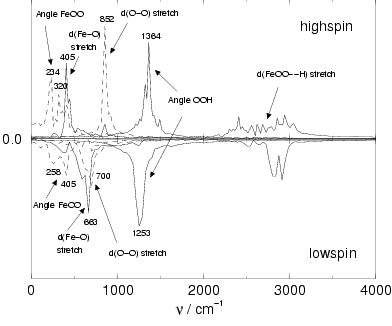The Fourier transformation of these velocity autocorrelation functions gives the vibration spectra shown in figure 6.3. The peaks shown in figure 6.3 are rather broad which is partly due to the relatively short simulation time (limited statistics). Nevertheless, the statistics are sufficient to clearly resolve the large differences between the low-spin and the high-spin spectra.

**Table 6.2:** Fe(III)OOH vibrations calculated for the hydrated complex in vacuo and in aqueous solution compared to experimental Raman frequencies of low-spin complexes (upper part) and high-spin complexes (lower part).

	$\angle$ FeOO	FeO	OO	$\angle$ OOH	OH

	low-spin calculations
(HO)Fe $^{\rm {III}}$ OOH (g)	253, 326	626	810	1291	3544

(HO)Fe $^{\rm {III}}$ OOH (aq)	258, 405	663	700	1253	2500-3000

	-experiment-
[(N4Py)Fe(OOH)] $^{2+}$		632	790
[(TPA)Fe(OOH)] $^{2+}$		626	789
[(TPEN)Fe(OOH)] $^{2+}$		617	796
[(trispicen)Fe(OOH)] $^{2+}$		625	801
[(trispicMeen)Fe(OOH)] $^{2+}$		617	796

	high-spin calculations
(HO)Fe $^{\rm {III}}$ OOH (g)	180, 209	445	980	1366	3514

(HO)Fe $^{\rm {III}}$ OOH (aq)	234, 320	405	852	1364	2000-3000

	-experiment-
[(TPEN)Fe(- $\eta^2$ -OO)] $^{2+}$		468	821
[(trispicMeen)Fe(- $\eta^2$ -OO)] $^{2+}$		468	820
[Fe(EDTA)(- $\eta^2$ -OO)] $^{3-}$		459	816
[Fe(EDTA)(- $\eta^2$ -OO)] $^{3-}$		472	824
Oxyhemerythrin(- $\eta^1$ -OOH)		503	844

This work: static DFT.

This work: AIMD including aqueous solution.

Ref HoRoHeFeQu99.

Ref GiBaSi00.

In frozen solution, Ref NeSo98.

In liquid solution at room temperature, Ref AhMcShApLoSa.

Ref ShLoSa.

The OH stretch vibration in the hydroperoxo ligand gives rise to a broad region of peaks around 2500-3000 cm $^{-1}$ in the

state, whereas these peaks are more localized in the low-spin state. In the simulation (and also in experiments[206]), the OH stretch frequency decreases when the hydrogen forms a hydrogen bond with a solvent water molecule. The shorter (stronger) the hydrogen bond, the lower the OH frequency. The average hydrogen bond length between the hydroperoxo hydrogen and the nearest solvent oxygen is 0.08 Å shorter in the high-spin state than in the low-spin state, while the average OH bond length in the hydroperoxo ligand is 0.01 Å longer. This could be an indication that the hydroperoxo ligand is more easily deprotonated in high-spin complexes, giving rise to the peroxo ligand, than in low-spin complexes.

The O-O stretch vibration decreases from 852 cm $^{-1}$ to 700 cm $^{-1}$ when going from the high-spin state to the low-spin state and the Fe-O stretch vibration increases from 405 cm $^{-1}$ to 663 cm $^{-1}$ , in agreement with the trend found with Raman spectroscopy for different complexes. For comparison, we have also optimized the geometry for the [Fe $^{\rm {III}}$ (H

(OOH)] $^{2+}$ complex in vacuo for the

state and the

state, and calculated the vibrational frequencies in the harmonic approximation. The results are shown in table 6.2, together with a compilation of values for the O-O and Fe-O stretch vibrations obtained using Raman spectroscopy on several low-spin and high-spin complexes. The O-O stretch vibration is significantly lower in the solvent than in the gas phase complex. This decrease, indicating a weakening of the O-O bond in aqueous solution, is due to the interaction of solvent water molecules with the hydroperoxo group. Not only the hydrogen, but also both oxygens are involved in hydrogen bonds with the solvent. Integration of the radial distribution functions (data not shown) obtained from the first 5 ps simulation of high-spin Fe(III)OOH in water (see previous paragraph) gives an average of 1.6 solvent hydrogens within a 2.3 Å radius of O $^\beta$ and 0.8 (other) solvent hydrogens within a 2.3 Å radius of O $^\alpha$ . Surprisingly, the static DFT results in vacuo for the low-spin O-O and Fe-O vibrations compare better with the experimental results than the ones obtained from the dynamics in aqueous solution at

K. This could be due to (again) the aqueous solvent interactions with the hydroperoxo ligand in the simulation, whereas the Raman spectroscopy studies using the hydrophobic pyridine based ligands as N4Py, TPA, TPEN, trispicen and trispicMeen typically took place in solvents such as acetone and acetonitrile. Another factor is of course the ligand field on the aqua ligated iron in the simulation, which is quite different from the ligand fields on iron complexed by these large nitrogen multidentate ligands used in the experiments. Comparison of our high-spin results with the only $\eta^1$ -OOH complex listed, namely oxyhemerythrin in aqueous solution, indicates that both factors could play a role: the Raman O-O stretch vibration agrees now much better with the AIMD result as in both results the solvent used is water which interacts with the hydroperoxo ligand, and secondly, the Fe-O stretch vibrations are still a bit off due to the different ligand field (note that oxyhemerythrin is a diiron species: L-Fe(III)-O-Fe(III)-OOH).

Concluding, we find that indeed the spin-state is an important factor for the O-O bond and Fe-O bond strengths in Fe(III)OOH complexes. The ligands (chelating agents) used in Fenton-like chemistry are therefore expected to directly influence the chemistry, because ligands inducing a large ligand field give rise to low-spin Fe(III)OOH complexes with stronger Fe-O bonds and weaker O-O bonds compared to the Fe-O and O-O bonds in the high-spin complexes which occur with ligands inducing a small ligand field. For the suggested second-step reactions following the initial Fe(III)OOH formation (reactions 6.4 till 6.6), the low-spin complexes thus promote the steps involving O-O lysis but make the steps involving Fe-O bond breaking even more unfavorable.