H
Transition metal catalyzed reactions are often assumed to start with
coordination of a reactant to the transition metal ion by a ligand
substitution reaction. If the substitution reaction is dissociative,
a vacant coordination site is first created, which is frequently
induced by thermal or photochemical means. The relative probability
of a dissociative mechanism for the substitution of a H![]() O ligand
for H
O ligand
for H![]() O
O![]() in the Fenton reaction is not known. However, rather
than starting from the coordinated H
in the Fenton reaction is not known. However, rather
than starting from the coordinated H![]() O
O![]() as in section 5.3.2,
we wish to investigate in the present section whether formation of an iron
oxo species is also probable when we start from a vacant coordination site
to which the hydrogen peroxide will coordinate in the first step of the reaction.
The energetic requirements will be essentially different
since the 23 kcal/mol bond energy of H
as in section 5.3.2,
we wish to investigate in the present section whether formation of an iron
oxo species is also probable when we start from a vacant coordination site
to which the hydrogen peroxide will coordinate in the first step of the reaction.
The energetic requirements will be essentially different
since the 23 kcal/mol bond energy of H![]() O
O![]() to pentaaquairon(II)
will become available in this first step. So in this section we present
the results of the AIMD simulation of a
reaction pathway for the reaction of hydrogen peroxide with an aqua
iron(II) complex containing a vacant coordination site.
Waiting for the spontaneous diffusion of
H
to pentaaquairon(II)
will become available in this first step. So in this section we present
the results of the AIMD simulation of a
reaction pathway for the reaction of hydrogen peroxide with an aqua
iron(II) complex containing a vacant coordination site.
Waiting for the spontaneous diffusion of
H![]() O
O![]() to the vacant iron site could take a very long time in an
AIMD simulation, simply because the reactants are as likely to
separate as to approach each other and secondly because the vacant
iron site is more likely to be occupied by one of the solvent water
molecules than by the single H
to the vacant iron site could take a very long time in an
AIMD simulation, simply because the reactants are as likely to
separate as to approach each other and secondly because the vacant
iron site is more likely to be occupied by one of the solvent water
molecules than by the single H![]() O
O![]() . To increase the probability
of observing a reactive encounter we need a favorable set of momenta for
the reactants and the solvating water molecules to start with. In the
following we will describe the method we used to obtain such a set of
momenta for a configuration of separated reactants in water followed
by the simulation of the reactive pathway.
. To increase the probability
of observing a reactive encounter we need a favorable set of momenta for
the reactants and the solvating water molecules to start with. In the
following we will describe the method we used to obtain such a set of
momenta for a configuration of separated reactants in water followed
by the simulation of the reactive pathway.
We started an AIMD simulation of the pentaaqua iron(II) hydrogen
peroxide complex in water, similar to the approach in the previous
section. As we now know, this complex is unstable against the iron(IV)
dihydroxo complex, so we constrained the H![]() O
O![]() oxygen-oxygen
bond distance to
oxygen-oxygen
bond distance to
![]() Å to prevent the
dissociation to occur. After an
equilibration time of 5 ps, we perturbed the system to force the
H
Å to prevent the
dissociation to occur. After an
equilibration time of 5 ps, we perturbed the system to force the
H![]() O
O![]() ligand to leave the complex and diffuse into the
solvent. There are several possibilities to make a ligand dissociate from
the complex, such as adding a potential
or changing the velocities of the iron complex and the H
ligand to leave the complex and diffuse into the
solvent. There are several possibilities to make a ligand dissociate from
the complex, such as adding a potential
or changing the velocities of the iron complex and the H![]() O
O![]() into
opposite directions. We, however, chose to shorten the Fe-O bond
distances for the five water ligands, which causes the complex to expel
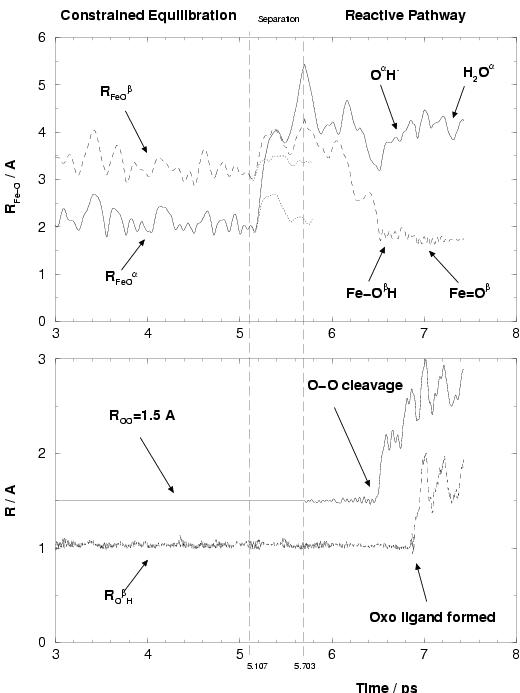
the hydrogen peroxide ligand. In figure 5.5, we
show the evolution of the two Fe-O (of Fe
into
opposite directions. We, however, chose to shorten the Fe-O bond
distances for the five water ligands, which causes the complex to expel
the hydrogen peroxide ligand. In figure 5.5, we
show the evolution of the two Fe-O (of Fe
![]() -H
-H![]() O
O![]() ) distances in the
upper graph, starting with the last two ps of the equilibration
phase. The lower graph shows the constrained O-O bond distance and the
HO
) distances in the
upper graph, starting with the last two ps of the equilibration
phase. The lower graph shows the constrained O-O bond distance and the
HO![]() distance, with
distance, with ![]() denoting the hydrogen peroxide
oxygen which is not bonded to iron (and
denoting the hydrogen peroxide
oxygen which is not bonded to iron (and ![]() denoting the other oxygen).
The shorter Fe-O
denoting the other oxygen).
The shorter Fe-O![]() distance
fluctuates around 2.11 Å which is slightly shorter than the average water
ligand Fe-O binding of 2.17 Å in this complex. We already expected
similar bonding properties for the H
distance
fluctuates around 2.11 Å which is slightly shorter than the average water
ligand Fe-O binding of 2.17 Å in this complex. We already expected
similar bonding properties for the H![]() O
O![]() and H
and H![]() O ligands from
the first bond dissociation energies in the gas phase complexes (see
table 5.2) being almost equal.
The hydrogen peroxide ligand is well solvated
by water molecules. Both hydrogens form hydrogen bonds to solvent water
molecules and also the oxygen O
O ligands from
the first bond dissociation energies in the gas phase complexes (see
table 5.2) being almost equal.
The hydrogen peroxide ligand is well solvated
by water molecules. Both hydrogens form hydrogen bonds to solvent water
molecules and also the oxygen O![]() accepts
on average 1 to 2 hydrogen bonds from solvent molecules.
accepts
on average 1 to 2 hydrogen bonds from solvent molecules.
|
At ![]() ps, we constrained the Fe-O distances of the
five water ligands at their actual value and shortened the bond length
in the following 100 steps (ca. 19.4 fs) to
ps, we constrained the Fe-O distances of the
five water ligands at their actual value and shortened the bond length
in the following 100 steps (ca. 19.4 fs) to ![]() Å. The result is that
the H
Å. The result is that
the H![]() O
O![]() ligand is expelled from the iron(II) coordination shell and moved
into the solvent, which is shown by the upper graph in figure
5.5. The dotted lines starting at
ligand is expelled from the iron(II) coordination shell and moved
into the solvent, which is shown by the upper graph in figure
5.5. The dotted lines starting at ![]() ps show
an unsuccessful attempt, where we shortened the five iron water
ligands distances to only
ps show
an unsuccessful attempt, where we shortened the five iron water
ligands distances to only ![]() Å. The solid and dashed lines,
however, show the successfully enforced dissociation, where especially
Å. The solid and dashed lines,
however, show the successfully enforced dissociation, where especially
![]() increases rapidly, within 600 fs, to a
distance of 5.4 Å. The other oxygen, O
increases rapidly, within 600 fs, to a
distance of 5.4 Å. The other oxygen, O![]() is hydrogen bonded to
2 solvent water molecules and also the hydrogen bonded to O
is hydrogen bonded to
2 solvent water molecules and also the hydrogen bonded to O![]() forms
a hydrogen bond to a solvent water, which makes this part of H
forms
a hydrogen bond to a solvent water, which makes this part of H![]() O
O![]() more
difficult to move and causes the H
more
difficult to move and causes the H![]() O
O![]() to rotate
during the separation, bringing
to rotate
during the separation, bringing ![]() furhter away from Fe than
furhter away from Fe than
![]() . At
. At ![]() ps, we now have a configuration of
separated reactants in water, with a set of momenta that will lead to
further separation. This configuration we take as the starting point
for our reaction pathway and we reverse all atomic velocities to
obtain a set of momenta that will lead to approaching reactants. Also,
the velocities of the fictitious plane wave coefficient dynamics are
reversed as well as the velocity of the Nosé thermostat variable.
We remove the H
ps, we now have a configuration of
separated reactants in water, with a set of momenta that will lead to
further separation. This configuration we take as the starting point
for our reaction pathway and we reverse all atomic velocities to
obtain a set of momenta that will lead to approaching reactants. Also,
the velocities of the fictitious plane wave coefficient dynamics are
reversed as well as the velocity of the Nosé thermostat variable.
We remove the H![]() O
O![]() oxygen-oxygen bond distance
constraint to allow dissociation to occur and also the five iron water
ligand bond distance constraints are removed. From this point we
start the simulation of the reaction pathway.
oxygen-oxygen bond distance
constraint to allow dissociation to occur and also the five iron water
ligand bond distance constraints are removed. From this point we
start the simulation of the reaction pathway.
The Verlet algorithm used for the integration of the equations of motion
is time reversible so that the system initially tracks back onto the ``forward''
trajectory of the separating reactants, when the velocities are reversed.
This can be seen from the symmetry of the
![]() plots in the upper graph (figure 5.5)
close to the mirror line at
plots in the upper graph (figure 5.5)
close to the mirror line at ![]() ps. However, due to the removal of
the bond distance constraints, the reversed trajectory diverges rapidly
from the forward path, as should be expected from the well-known Lyapunov
instability of MD trajectories towards small differences in the initial
conditions. In fact, the trajectory followed by the approaching reactants is so
much different from the trajectory followed by the separating reactants that
now the other H
ps. However, due to the removal of
the bond distance constraints, the reversed trajectory diverges rapidly
from the forward path, as should be expected from the well-known Lyapunov
instability of MD trajectories towards small differences in the initial
conditions. In fact, the trajectory followed by the approaching reactants is so
much different from the trajectory followed by the separating reactants that
now the other H![]() O
O![]() oxygen O
oxygen O![]() forms a bond with
the iron(II) complex at
forms a bond with
the iron(II) complex at ![]() ps, i.e. 0.8 ps after the
velocities were reversed.
Almost immediately after the Fe-O
ps, i.e. 0.8 ps after the
velocities were reversed.
Almost immediately after the Fe-O![]() bond is formed the H
bond is formed the H![]() O
O![]() dissociates, which can be seen from the increasing
dissociates, which can be seen from the increasing
![]() and
and
![]() after
after ![]() ps in figure 5.5.
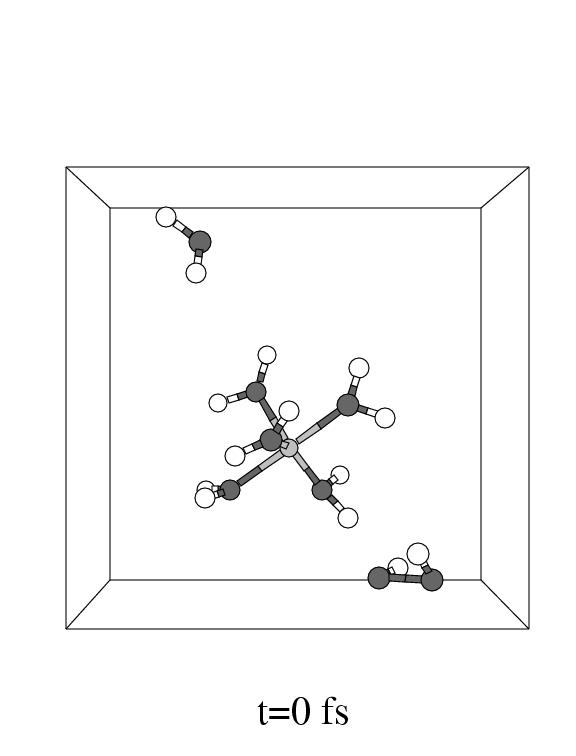
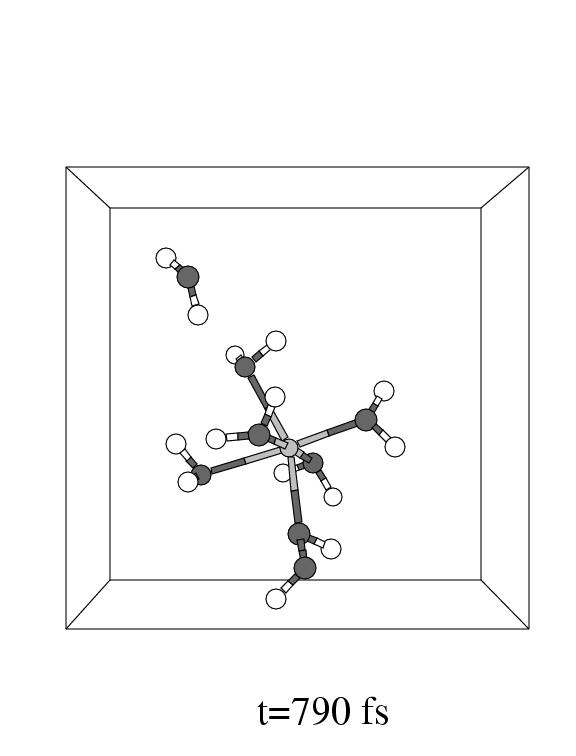
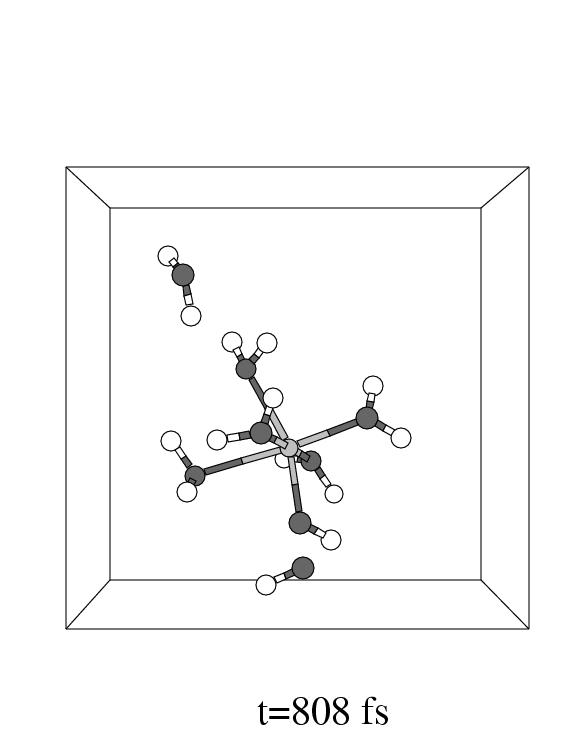
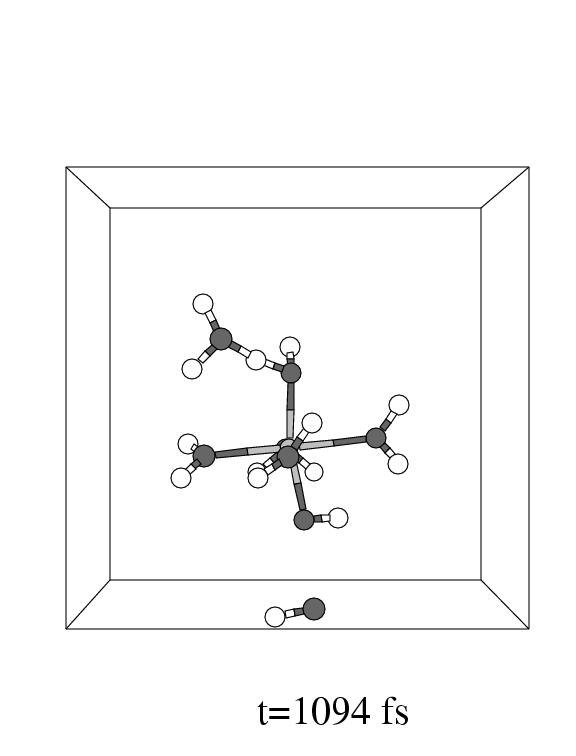
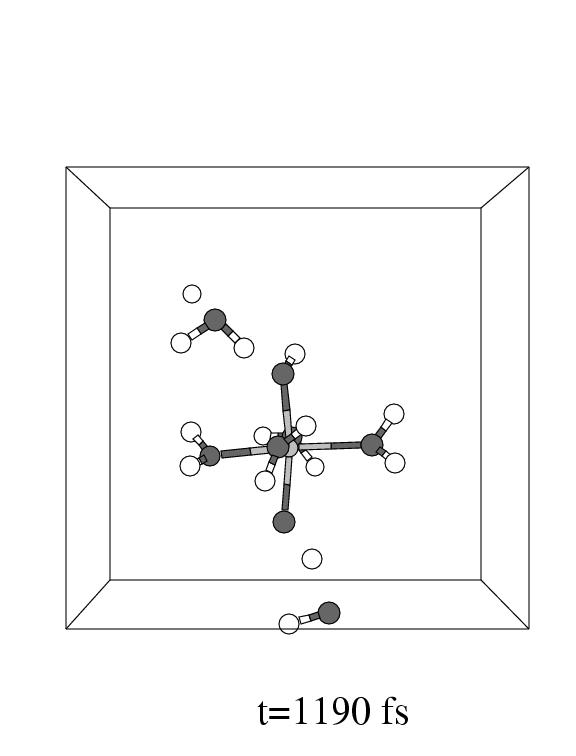
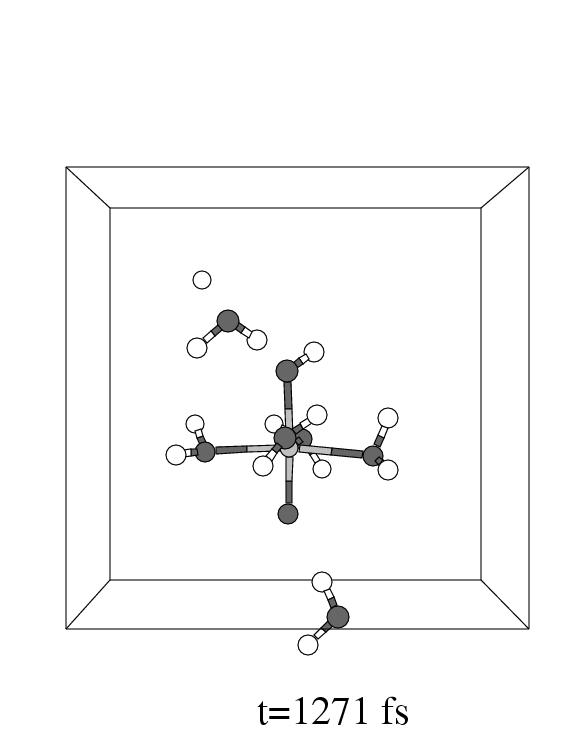
The first three pictures in figure 5.6 show snapshots
of the system (with omission of all solvent water molecules, except one, for
clarity) during this coordination process.
Note that the incoming hydrogen peroxide, in the lower part of the unit cell
in panel 1, to the right, enters the vacant coordination site of the pentaaqua
Fe(II) complex in panel 2. Apparently, the incoming hydrogen peroxide does not
equilibrate in the local minimum representing the iron hydrogen peroxide complex,
but instead it dissociates as soon as the iron oxygen distance reaches the short
value of 2.1 Å forming the (formally) Fe
ps in figure 5.5.
The first three pictures in figure 5.6 show snapshots
of the system (with omission of all solvent water molecules, except one, for
clarity) during this coordination process.
Note that the incoming hydrogen peroxide, in the lower part of the unit cell
in panel 1, to the right, enters the vacant coordination site of the pentaaqua
Fe(II) complex in panel 2. Apparently, the incoming hydrogen peroxide does not
equilibrate in the local minimum representing the iron hydrogen peroxide complex,
but instead it dissociates as soon as the iron oxygen distance reaches the short
value of 2.1 Å forming the (formally) Fe![]() -OH
-OH![]() complex
and a hydroxyl radical.
The much shorter average iron hydroxo ligand bond
length of
complex
and a hydroxyl radical.
The much shorter average iron hydroxo ligand bond
length of
![]() Å and the higher frequency compared
to the Fe-O bond of a H
Å and the higher frequency compared
to the Fe-O bond of a H![]() O
O![]() or H
or H![]() O ligand confirm that indeed the
O
O ligand confirm that indeed the
O![]() H. brought
the iron to the higher oxidation state of +3, increasing the bond strength by
the extra electrostatic attraction. About 350 fs after the O
H. brought
the iron to the higher oxidation state of +3, increasing the bond strength by
the extra electrostatic attraction. About 350 fs after the O![]() H.
radical is formed, it is attracted by the hydrogen of the O
H.
radical is formed, it is attracted by the hydrogen of the O![]() H
H![]() hydroxo ligand, which is abstracted about
50 fs later to form a water molecule and the ferryl ion moiety.
The average Fe
hydroxo ligand, which is abstracted about
50 fs later to form a water molecule and the ferryl ion moiety.
The average Fe![]() =O
=O![]() bond length of 1.72 Å is even shorter than
the iron-oxygen bond in the Fe
bond length of 1.72 Å is even shorter than
the iron-oxygen bond in the Fe![]() -OH
-OH![]() complex (see again
figure 5.5) and also the frequency increases
with 100-200 cm
complex (see again
figure 5.5) and also the frequency increases
with 100-200 cm![]() to roughly 700 cm
to roughly 700 cm![]() (the statistics do not allow
for an accurate number for the frequency).
Again, we have found the spontaneous formation of the ferryl ion.
(the statistics do not allow
for an accurate number for the frequency).
Again, we have found the spontaneous formation of the ferryl ion.
|
One of the side effects of the increasing oxidation state of the iron complex, going
from 2+ to 4+ during the reactive pathway, is that the acidity of the complex
increases. We have already seen this phenomenon in the simulation described in the
previous section. Again, as shown in the last three snapshots in figure
5.6, hydrolysis of one water ligand takes place at a
time somewhere between the moment that the Fe
![]() complex was
formed and the momemt that Fe
complex was
formed and the momemt that Fe
![]() was formed.
So also in this reactive pathway we end up with the [(H
was formed.
So also in this reactive pathway we end up with the [(H![]() O)
O)![]() Fe(IV)(OH)(O)]
Fe(IV)(OH)(O)]![]() complex and an extra proton in the solvent.
complex and an extra proton in the solvent.
Although the same iron(IV)oxo complex is formed as in the previous
simulations starting from the equilibrated pentaaqua iron(II) hydrogen
peroxide complex, there is a difference in the mechanism.
In the previous sections, we have seen the formation of the dihydroxo iron(IV)
complex as the initial step, as was also predicted by our gas phase study.
The iron(IV)oxo complex (ferryl ion) can then be formed in a second step
by hydrolysis of an hydroxo ligand
(as demonstrated by our first simulation, section 5.3.2).
Instead, in the present simulation starting from separated reactants,
the ferryl ion is formed via a more direct mechanism. The OH. radical
does not find a fast terminating route along an H-bond wire to a water ligand to form a
dihydroxo complex, but stays in the neighborhood of the formed
OH![]() ligand and then finds a quenching pathway by abstracting its hydrogen
after roughly 0.3 ps.
Apparently, in this case, a pathway to quench the radical in concertation with
the O-O bond cleavage and make the process exothermic is not necessary.
Indeed, in the present simulation, the energy balance is different.
Starting from coordinated H
ligand and then finds a quenching pathway by abstracting its hydrogen
after roughly 0.3 ps.
Apparently, in this case, a pathway to quench the radical in concertation with
the O-O bond cleavage and make the process exothermic is not necessary.
Indeed, in the present simulation, the energy balance is different.
Starting from coordinated H![]() O
O![]() (section 5.3.2) the energy
needed for the OH. formation is equal to the energy needed to dissociate
the oxygen-oxygen bond of H
(section 5.3.2) the energy
needed for the OH. formation is equal to the energy needed to dissociate
the oxygen-oxygen bond of H![]() O
O![]() (A in table 5.2)
minus the energy gain of replacing the Fe
(A in table 5.2)
minus the energy gain of replacing the Fe
![]() -H
-H![]() O
O![]() bond
with the much stronger Fe
bond
with the much stronger Fe
![]() -OH bond (C-D).
Starting with a vacant coordination site and H
-OH bond (C-D).
Starting with a vacant coordination site and H![]() O
O![]() in solvation (the
present simulation) leaves us with an extra 23 kcal/mol (neglecting the solvent
effects), which is enough to form the OH. radical without the
need of a fast transfer to an exothermic termination.
in solvation (the
present simulation) leaves us with an extra 23 kcal/mol (neglecting the solvent
effects), which is enough to form the OH. radical without the
need of a fast transfer to an exothermic termination.
The reactive pathways presented in this work illustrate possible
microscopic routes via which the chemical reactions could take place.
In a next study, will test how realistic the last pathway, illustrating
coordination and reaction of H![]() O
O![]() with iron(II), is, by initiating
many new reactive trajectories from this last pathway using the method
of transition path sampling.
with iron(II), is, by initiating
many new reactive trajectories from this last pathway using the method
of transition path sampling.