In this section, we present the results for the methane-to-methanol
oxidation by the aqua iron(IV)oxo species, following the oxygen-rebound
mechanism. This mechanism consists of two steps: first the hydrogen abstraction
from methane by the iron(IV)oxo species, producing iron(III)hydroxo and
a .CH![]() radical, and second, the collapse of the .CH
radical, and second, the collapse of the .CH![]() radical
onto the iron(III)hydroxo oxygen, forming Fe(II)CH
radical
onto the iron(III)hydroxo oxygen, forming Fe(II)CH![]() OH.
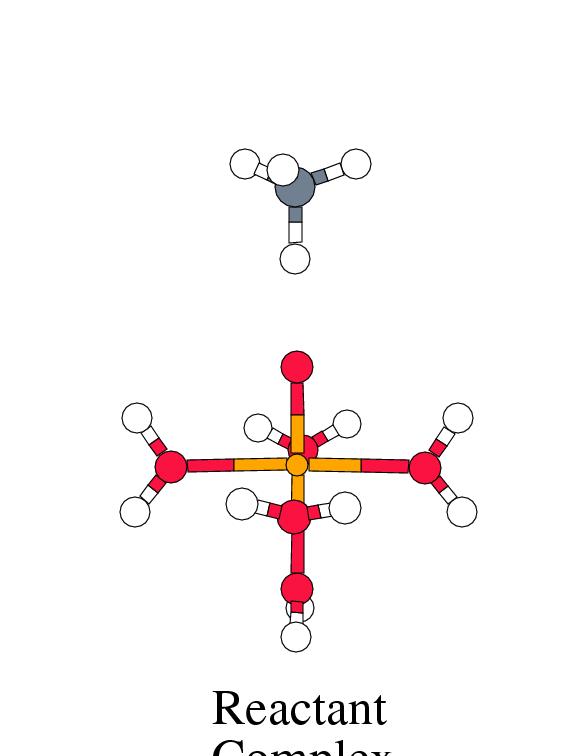
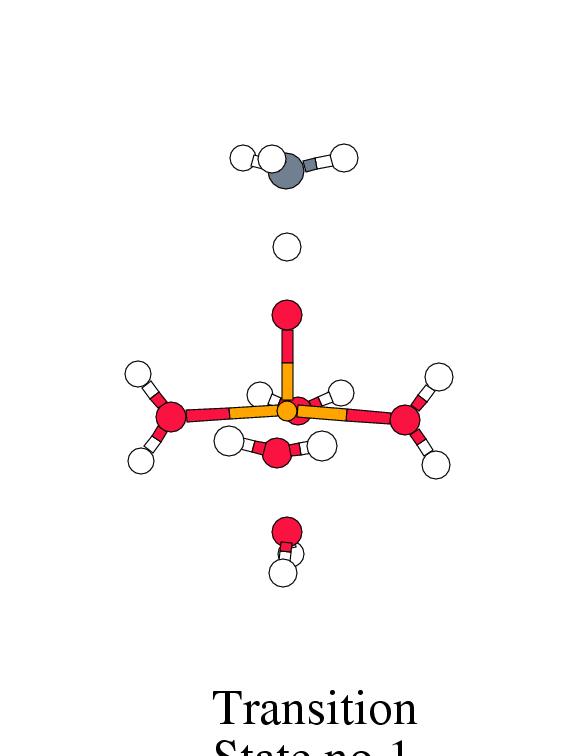
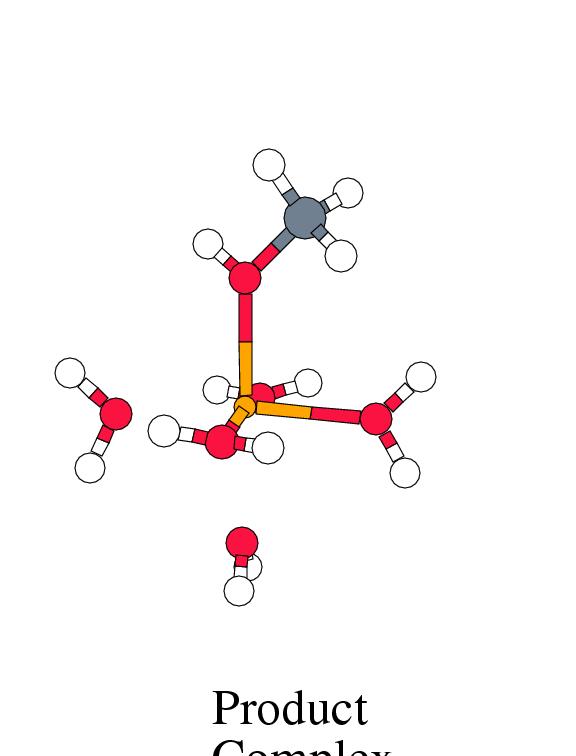
Figure 8.2 shows the energy profile for
these reaction steps along with the intermediate complex geometries.
For this mechanism, we have also computed the zero-point energy corrections, the
temperature dependent enthalpy corrections for a temperature of
OH.
Figure 8.2 shows the energy profile for
these reaction steps along with the intermediate complex geometries.
For this mechanism, we have also computed the zero-point energy corrections, the
temperature dependent enthalpy corrections for a temperature of ![]() K
and the entropy term
K
and the entropy term ![]() (see table 8.3),
the sum of which is added to the internal energy to give the
free energy, indicated in figure 8.2 between
parentheses.
(see table 8.3),
the sum of which is added to the internal energy to give the
free energy, indicated in figure 8.2 between
parentheses.
[width=77mm] 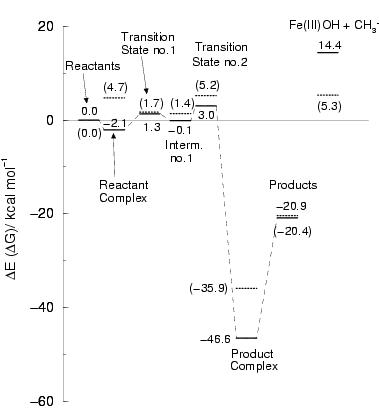
|
|
|
|||||||
| Reactant | Trans. | Inter- | Free | Trans. | Product | Free | |
| Complex | State 1 | mediate | Radic. | State 2 | Complex | Products | |
|
|
|||||||
|
Fenton |
-2.1 | 1.3 | -0.1 | 14.4 | 3.0 | -46.6 | -20.9 |
|
MMO |
2.3 | 13.8 | 2.8 | 7.6 | -47.7 | ||
|
MMO |
-1.5 | 23.2 | 11.3 | 23.7 | 20.6 | -41.8 | -34.3 |
|
P450 |
-1.0 | 26.7 | 23.6 | 29.1 | -36.9 | ||
|
|
|||||||
|
|
-0.8 | -4.9 | -3.3 | -3.9 | -3.5 | 1.8 | 0.1 |
|
|
0.4 | -4.4 | -1.7 | -1.8 | -2.1 | 4.2 | -1.3 |
|
|
7.2 | 9.7 | 6.6 | -3.4 | 7.8 | 4.6 | 1.7 |
|
|
||||||||
| Free | React. | Trans. | Inter- | Free | Trans. | Prod. | Free | |
| React. | Comp. | State 1 | mediate | Radic. | State 2 | Comp. | Prod. | |
|
|
||||||||
|
|
1.61 | 1.63 | 1.72 | 1.77 | 1.77 | 1.79 | 2.09 | |
|
|
2.91 | 2.55 | 2.78 | 2.50 | 1.47 | |||
|
|
1.76 | 1.20 | 1.03 | 0.98 | 1.01 | 0.97 | 1.43 | |
|
|
1.10 | 1.15 | 1.34 | 1.76 | 1.70 | 1.99 | 0.97 | |
|
|
1. | 0. | 1. | 30. | 108. | 108. | ||
|
|
179. | 176. | 155. | 179. | 151. | 120. | ||
|
|
||||||||
|
|
1.35 | 1.36 | 1.46 | 1.43 | 1.49 | 1.43 | 1.30 | 1.33 |
|
|
-0.20 | -0.30 | -0.48 | -0.36 | -0.25 | -0.37 | -0.08 | -0.09 |
|
|
0.30 | 0.34 | 0.34 | 0.30 | 0.00 | 0.33 | 0.30 | 0.22 |
|
|
0.08 | 0.13 | 0.32 | 0.32 | 0.00 | 0.34 | 0.21 | 0.02 |
|
|
-0.08 | -0.11 | 0.04 | -0.03 | 0.07 | -0.02 | 0.05 | 0.07 |
|
|
||||||||
|
|
3.14 | 3.40 | 3.97 | 4.11 | 4.20 | 4.08 | 3.83 | 3.85 |
|
|
0.69 | 0.59 | 0.38 | 0.40 | 0.52 | 0.35 | 0.04 | 0.00 |
|
|
0.00 | -0.10 | -0.50 | -0.75 | 1.08 | -0.65 | 0.00 | 0.00 |
|
|
0.00 | -0.04 | -0.03 | -0.01 | 0.03 | -0.01 | 0.00 | 0.00 |
|
The interaction between the methane substrate and the iron(IV)oxo complex
is again very weak, equal to ![]() 2 kcal/mol. The first reaction step, the
transfer of a CH
2 kcal/mol. The first reaction step, the
transfer of a CH![]() hydrogen from methane to the oxo ligand, forming an
Fe(III)OH complex with a bound .CH
hydrogen from methane to the oxo ligand, forming an
Fe(III)OH complex with a bound .CH![]() radical, is surprisingly easy.
The overall reaction energy is
radical, is surprisingly easy.
The overall reaction energy is ![]() kcal/mol, and the barrier is only
3.4 kcal/mol (1.3 kcal/mol with respect to the free reactants).
Release of the .CH
kcal/mol, and the barrier is only
3.4 kcal/mol (1.3 kcal/mol with respect to the free reactants).
Release of the .CH![]() group, producing a free radical,
was calculated from the energy difference of the separate geometry
optimized structures to cost 14.4 kcal/mol. In contrast to H-abstraction
from an isolated CH
group, producing a free radical,
was calculated from the energy difference of the separate geometry
optimized structures to cost 14.4 kcal/mol. In contrast to H-abstraction
from an isolated CH![]() molecule which costs 103 kcal/mol
(calculated at the DFT-BP+ZPE level of theory), the energy surface is very
flat due to the simultaneous formation of the OH bond with the breaking
of the CH bond. Also compared to the formation of the free .CH
molecule which costs 103 kcal/mol
(calculated at the DFT-BP+ZPE level of theory), the energy surface is very
flat due to the simultaneous formation of the OH bond with the breaking
of the CH bond. Also compared to the formation of the free .CH![]() radical
from the reactant complex, which costs 16.5 kcal/mol, the reaction
energy needed to go from Fe(IV)O
radical
from the reactant complex, which costs 16.5 kcal/mol, the reaction
energy needed to go from Fe(IV)O![]() HCH
HCH![]() to Fe(III)OH
to Fe(III)OH![]() CH
CH![]() is very small. This is obviously due to fairly strong (14.5 kcal/mol) bond between
the .CH
is very small. This is obviously due to fairly strong (14.5 kcal/mol) bond between
the .CH![]() radical and the Fe(III)OH complex. We have not analyzed this
bond in detail, but we note that there is a significant charge transfer contribution
from CH
radical and the Fe(III)OH complex. We have not analyzed this
bond in detail, but we note that there is a significant charge transfer contribution
from CH![]() to the iron complex concomitant with the H-abstraction
(see also the substantial absolute increase of
to the iron complex concomitant with the H-abstraction
(see also the substantial absolute increase of ![]() O and
O and ![]() CH
CH![]() as
as ![]() OH decreases
and
OH decreases
and ![]() CH increases in table 8.4, whereas the charge
on CH
CH increases in table 8.4, whereas the charge
on CH![]() becomes zero for the free radical formation).
becomes zero for the free radical formation).
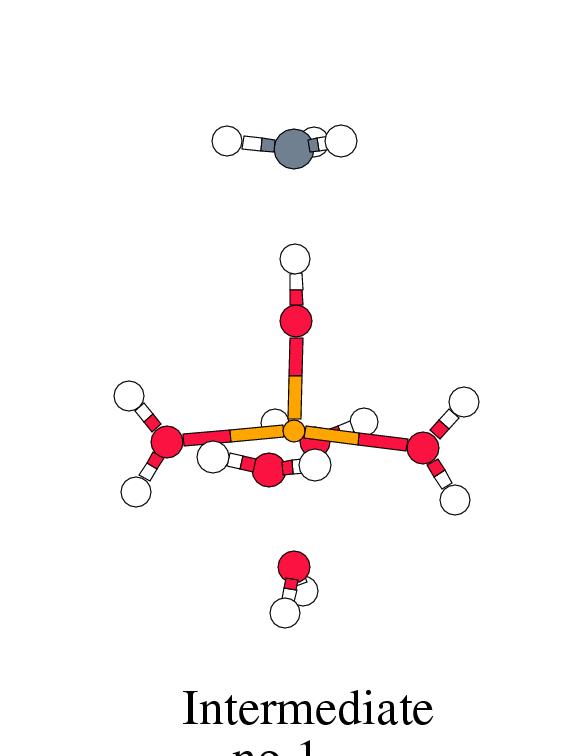
For the second step in the oxygen-rebound mechanism,
we find the formation of methanol bound to pentaaqua iron(II) to be very
exothermic (46.6 kcal/mol), with again a very small barrier,
equal to 3.1 kcal/mol. We did not
succeed in finding this second transition state from geometry optimization
along the unstable mode of the Hessian, due to convergence problems
(which is a notorious problem of weakly bound radicals to transition
metal complexes, see e.g. ref. Si01). However, from the
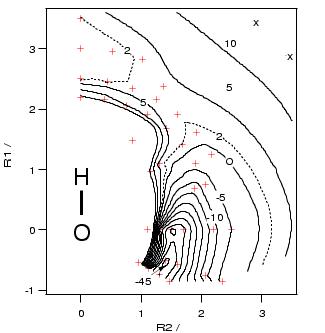
potential energy surface shown in figure 8.3, we could
determine the transition state structure to be the one shown in
figure 8.2. This potential energy surface
was computed from a geometry optimization for each point (indicated
by the crosses) constraining only the C-O bond distance and the H-O-C
angle. The oxygen of the hydroxo complex is situated at the coordinates
(0,0) in the plot and the ![]() axis is depicted to be along O-H.
The energy of the Fe
axis is depicted to be along O-H.
The energy of the Fe![]() -OH
-OH![]() CH
CH![]() intermediate, which is a local minimum on the energy surface,
was set to zero in figure 8.2
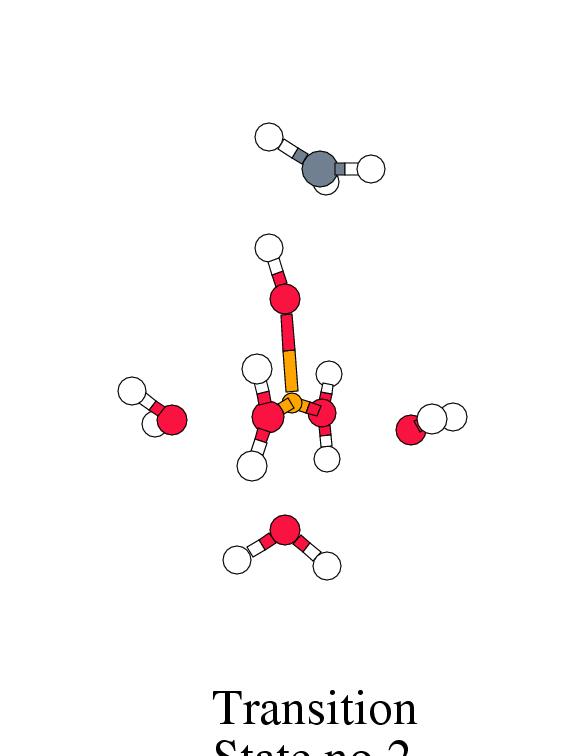
The potential energy surface shows that there exists a
narrow channel, through which the bound methyl radical can rotate around the
hydroxo hydrogen to bind with the oxygen. The channel is very flat up to an
H-O-C angle of about 60 degrees, with a small maximum at an angle of
30 degrees (transition state no.2), but then enters a very steep well
associated with the irreversible formation of methanol. From the
zero-Kelvin energy, this second step seems thus much more likely than
formation of the free methyl radical.
However, if we include zero-point energy effects, temperature corrections
and entropy effects, we see that the free energy barriers are similar,
namely 5.2 and 5.3 kcal/mol, respectively (see figure 8.2).
intermediate, which is a local minimum on the energy surface,
was set to zero in figure 8.2
The potential energy surface shows that there exists a
narrow channel, through which the bound methyl radical can rotate around the
hydroxo hydrogen to bind with the oxygen. The channel is very flat up to an
H-O-C angle of about 60 degrees, with a small maximum at an angle of
30 degrees (transition state no.2), but then enters a very steep well
associated with the irreversible formation of methanol. From the
zero-Kelvin energy, this second step seems thus much more likely than
formation of the free methyl radical.
However, if we include zero-point energy effects, temperature corrections
and entropy effects, we see that the free energy barriers are similar,
namely 5.2 and 5.3 kcal/mol, respectively (see figure 8.2).
This rebound mechanism has also been theoretically predicted to be the
reaction mechanism for the methane-to-methanol oxidation by the enzymes
P450 and MMO (as aforementioned in the introduction).
In these complexes, a Fe![]() O
species is ligated by either a porphyrin ring via four nitrogens (P450) or
octahedrally by none-heme ligands via connecting oxygens (MMO), which makes especially
the latter interesting to compare our results with. Literature
values for the energetics are compiled along with our results in
table 8.3. We see that also in these biological
complexes the methane is initially very weakly bound in the reactant complex
and that the overall formation of the product complex is very exothermic.
The reaction barriers in between, however, are significantly higher for the
oxidation by the enzymes than by the aqua ligated iron oxo species. For methane
oxidation by P450,
Ogliaro et al. found a barrier of 26.7 kcal/mol for the hydroxylation,
and 29.1 kcal/mol for the rebound step, although the latter barrier vanishes
if the system is allowed to cross to the low-spin surface[160].
Cytochrome P450 is known to be incapable of oxidizing methane, in contrast
to MMO. Still, Basch et al find a barrier for H-abstraction by MMO which is
almost as high as the one for P450, equal to 23.2 kcal/mol[186].
Siegbahn found a much lower barrier with MMO, namely 13.8 kcal/mol, which is still
11 kcal/mol higher than the barrier we find for the oxidation with aqua iron
oxo[185]. The cited work on P450 and MMO was performed using the hybrid
B3LYP functional, which is known to sometimes give better transition state energies
in cases where these barriers are underestimated by GGA functionals, see for
example ref. bernd2.
However, a comparison of these two functionals for the hydroxylation of H
O
species is ligated by either a porphyrin ring via four nitrogens (P450) or
octahedrally by none-heme ligands via connecting oxygens (MMO), which makes especially
the latter interesting to compare our results with. Literature
values for the energetics are compiled along with our results in
table 8.3. We see that also in these biological
complexes the methane is initially very weakly bound in the reactant complex
and that the overall formation of the product complex is very exothermic.
The reaction barriers in between, however, are significantly higher for the
oxidation by the enzymes than by the aqua ligated iron oxo species. For methane
oxidation by P450,
Ogliaro et al. found a barrier of 26.7 kcal/mol for the hydroxylation,
and 29.1 kcal/mol for the rebound step, although the latter barrier vanishes
if the system is allowed to cross to the low-spin surface[160].
Cytochrome P450 is known to be incapable of oxidizing methane, in contrast
to MMO. Still, Basch et al find a barrier for H-abstraction by MMO which is
almost as high as the one for P450, equal to 23.2 kcal/mol[186].
Siegbahn found a much lower barrier with MMO, namely 13.8 kcal/mol, which is still
11 kcal/mol higher than the barrier we find for the oxidation with aqua iron
oxo[185]. The cited work on P450 and MMO was performed using the hybrid
B3LYP functional, which is known to sometimes give better transition state energies
in cases where these barriers are underestimated by GGA functionals, see for
example ref. bernd2.
However, a comparison of these two functionals for the hydroxylation of H![]() by a bare iron oxo species showed that there is good agreement on the
reaction barriers among the B3LYP and BP86 functionals, although the overall
reaction exothermicy was found to be 10 kcal/mol smaller by the BP86 functional
compared to the B3LYP functional[168]. Since discrepancies between the
functionals
are typically amplified in such small bare atom reactions, we expect
much smaller discrepancies between energetics calculated with B3LYP and BP86 for
the present complexes.
by a bare iron oxo species showed that there is good agreement on the
reaction barriers among the B3LYP and BP86 functionals, although the overall
reaction exothermicy was found to be 10 kcal/mol smaller by the BP86 functional
compared to the B3LYP functional[168]. Since discrepancies between the
functionals
are typically amplified in such small bare atom reactions, we expect
much smaller discrepancies between energetics calculated with B3LYP and BP86 for
the present complexes.
The O-H and C-H distances in the first transition state (i.e. the one
for the hydroxylation step) (see
table 8.4) are very similar to those found for the
biochemical hydroxylations. For MMO, Siegbahn found ![]() =1.24 Å
and
=1.24 Å
and ![]() =1.30 Å, and Basch et al found
=1.30 Å, and Basch et al found ![]() =1.21 Å
and
=1.21 Å
and ![]() =1.33 Å, which compares well with
the ones in our transition state (
=1.33 Å, which compares well with
the ones in our transition state (![]() =1.20 Å and
=1.20 Å and
![]() =1.34 Å). For the P450 transition state, Ogliaro et al found
=1.34 Å). For the P450 transition state, Ogliaro et al found
![]() =1.09 Å and
=1.09 Å and ![]() =1.50 Å, which lies relatively
closer to the Fe
=1.50 Å, which lies relatively
closer to the Fe![]() -OH
-OH![]() CH
CH![]() intermediate state.
Summarizing, we find that, apart from the higher barrier for hydroxylation
in the MMO case, the rebound mechanism for methane-to-methanol oxidation
by the pentaaqua iron(IV)oxo species is quite similar to the mechanism
for the methane oxidation by MMO, calculated by Siegbahn. The hydrated ferryl ion
in vacuo is found to be a highly reactive species, very well capable of
hydroxylation and oxidation reactions with an organic substrate.
intermediate state.
Summarizing, we find that, apart from the higher barrier for hydroxylation
in the MMO case, the rebound mechanism for methane-to-methanol oxidation
by the pentaaqua iron(IV)oxo species is quite similar to the mechanism
for the methane oxidation by MMO, calculated by Siegbahn. The hydrated ferryl ion
in vacuo is found to be a highly reactive species, very well capable of
hydroxylation and oxidation reactions with an organic substrate.