Determination of the transition state on the initial reaction path

In the original transition path sampling procedure, to determine the transition state of a single reaction pathway, a large number of trajectories have to be initiated with random initial atomic velocities from some trial point along the pathway. From the ratio of the number of trajectories that end in the reactant well and the number of trajectories that end in the product well, it can be determined whether the trial point is located on the reactant side or the product side of the TS point. If more than 50 % of the trajectories ended in the reactant well, a new trial point is chosen located at the product side of the previous point (and vice versa), and this procedure is repeated until the TS point is found for which 50 % of the trajectories generated from this point end up in the reactant well and 50 % end up in the product well. Unfortunately, this technique is computationally very expensive in combination with Car-Parrinello MD for our system. Therefore, we introduce an alternative strategy to speed up the search for the TS point. Instead of branching off many trajectories from a trial point with random initial atomic velocities, we start one trajectory with zero atomic velocities. The initial direction of the system is therefore determined by the potential energy rather than the free energy, as was the case in the original strategy. If the system ends up in the reactant state, we try a new trial point located more to the products side along the pathway and vice versa. Due to the low temperature the system will have (starting from zero Kelvin) and since mainly the starting direction of the generated trajectory is relevant, a damped Nosé thermostat which heats up the system to

K is used to accelerate the search even more. Since we are however interested in the free energy transition state position, we will in the end nevertheless use the original generation procedure to find the exact location, but our ``zero Kelvin'' approach provides a very cheap means to obtain a good first guess for the expensive full procedure.

**Figure 7.3:** Left-hand-side: estimation of the position of the transition state on the reaction path (bold line) by starting new trajectories from certain configurations (denoted with crosses) with zero velocities. Solid lines indicate trajectories which recross back to the reactant state; dashed lines are paths which lead to oxygen-oxygen lysis (products). Right-hand-side: testing the TS position estimate by initiating 20 trajectories with random velocities, starting in between point 4 and 5 of the left-hand-side trajectories. Indeed, half of them end up in the reactant state, and half in the product state.

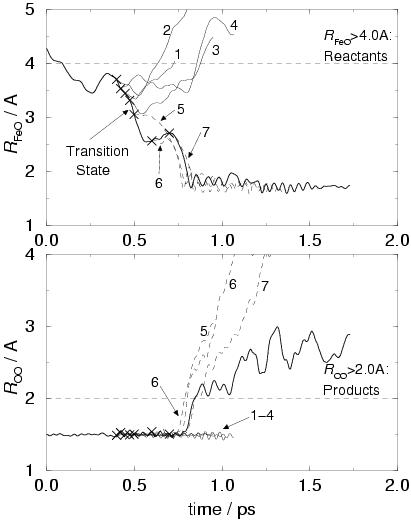
The left-hand-side graphs in figure 7.3, show the result of our ``zero Kelvin'' approach to narrow down the TS position on our initial pathway, defined in section 7.2, of the reaction between pentaaqua iron(II) and hydrogen peroxide in water. Note that the starting point of our initial path at

ps in figure 7.1 has been set to

in figure 7.3. The upper left-hand-side graph shows again the iron(II) oxygen distance (bold line), which equals $R_{\rm {FeO}}=4.3$ Å at the start at

and decreases to $R_{\rm {FeO}}=1.9$ Å 800 femtoseconds later, as hydrogen peroxide coordinates and bonds to iron and the oxygen-oxygen bond breaks (which is shown in the lower graph). The horizontal dashed lines depict our choice for the order parameters that define the stable states. That is, for $R_{\rm {FeO}^\alpha}>4.0$ Å the system finds itself in the reactant well of separated iron(II) and hydrogen peroxide and for $R_{\rm {OO}}>2.0$ Å the system finds itself in the product well of dissociated hydrogen peroxide. Note that this definition imposes no constraints--the final product may consist of the OH. radical, a dihydroxo or oxo iron complex or something we had not thought of yet.

The crosses on the bold line in both of the left-hand-side graphs denote the trial points, from which trajectories were started with zero velocities. We see that the trajectories originating from the first four trial points all end up in the reactant well of $R_{\rm {FeO}}>4.0$ Å (solid lines). The trajectories of the next three points all end up in the product state of $R_{\rm {OO}}>2.0$ Å (dashed lines). We have thus narrowed down the estimate for the TS location between the fourth point at

ps ( $R_{\rm {FeO}}=3.3$ Å) and the fifth point at

ps ( $R_{\rm {FeO}}=3.1$ Å).

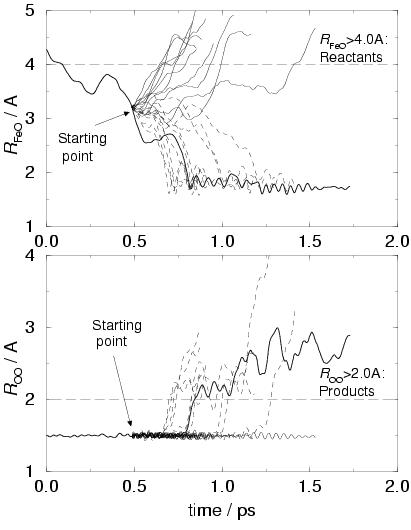
To verify this estimate of the TS location, we started 20 AIMD trajectories at the point at

ps (in the middle between point 4 and 5) where the iron-oxygen separation is $R_{\rm {FeO}}=3.21$ Å. The initial atomic momenta were drawn from a gaussian (Boltzmann) distribution of a temperature of

K and corrected for any total momentum of the system. In the right-hand-side graphs of figure 7.3, the 20 trajectories have been plotted. Ten of them end up in the reactant well and the other ten end up in the product well. Perhaps a little fortuitously, apparently our approach resulted in a very good estimate of the transition state location on our reaction pathway, which could indicate that the TS point on the free energy surface (sampled by the original method, starting with random momenta) is not very different from the TS point on the potential energy surface (which determines the TS position resulting from our zero-Kelvin approach).

The large iron-oxygen separation of $R_{\rm {FeO}}=3.21$ Å and the unchanged O-O distance in the transition state configuration indicates that the barrier is mainly determined by the solvent environment for our reaction pathway and not by the actual oxygen-oxygen lysis. Earlier, we had inferred that this barrier for hydrogen peroxide coordinated to iron(II) in aqueous solution must be small in the PAW calculation as we observed the spontaneous reaction to the ferryl ion or to an iron(IV)dihydroxo complex, during AIMD simulations[144,171]. Also in the present simulation the barrier for O-O bond breaking is apparently small. It is possible that the barrier is underestimated in the PAW calculation, in view of the overestimation of higher oxidation states for iron as mentioned earlier in section 7.3. In ADF calculations (STO basis functions) for the isolated complex we have found a barrier, although a small one (6 kcal/mol), for the O-O lysis of the coordinated hydrogen peroxide in the pentaaqua iron hydrogen peroxide complex. The TS barrier in this case was found when the leaving O $^{\beta}$ H radical was in the process of forming a bond to a H atom of an adjacent ligand, the calculations in vacuo preventing it to go into solution.[145] The TS position found in the present CPMD simulation in solution is clearly connected to a barrier in the ligand coordination process. This can be understood assuming that the approaching hydrogen peroxide has to break (partially) with the energetically favorable solvation shell before it can form an energetically favorable bond with the iron complex. The correspondence between the methods to estimate the TS position (namely ``random momenta'' and ``zero-Kelvin'') can be understood in the same way when we also assume that the entropy loss due to coordination is less important. For comparison, the free energy barrier for exchange of a water molecule from the first coordination shell of iron(II) in water was estimated to be 8.6 kcal/mol with NMR spectroscopy, which is indeed mainly energetic ( $\Delta H^\ddagger=7.7$ kcal/mol, $-T \Delta S^\ddagger=0.9$ kcal/mol)[215].