The reaction equilibrium constant and the transition state theory estimate of
the reaction rate of a chemical reaction are determined by the free-energy profile
along the reaction path. The free energy reaction barrier is the
reversible work necessary to bring the system from the stable state of reactants
(RS) to the transition state (TS). We will characterize these states by some order
parameter, a reaction coordinate ![]() , which is a function of the positions of
the nuclei. As the reversible work is independent of the path, the precise choice
of the reaction coordinate is not crucial, but a practical and physically
appealing choice is one that incorporates the asymmetric stretch vibration along the
Cl-C-Cl axis of the transition state complex CH
, which is a function of the positions of
the nuclei. As the reversible work is independent of the path, the precise choice
of the reaction coordinate is not crucial, but a practical and physically
appealing choice is one that incorporates the asymmetric stretch vibration along the
Cl-C-Cl axis of the transition state complex CH![]() Cl
Cl![]() .
Given a choice for the reaction coordinate, wa can obtain the free
energy change
.
Given a choice for the reaction coordinate, wa can obtain the free
energy change ![]() along the reaction path, using
the technique of thermodynamic integration (see e.g. ref frenkel_smit):
along the reaction path, using
the technique of thermodynamic integration (see e.g. ref frenkel_smit):
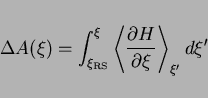 |
(47) |
Here ![]() is the Hamiltonian of the system of nuclei, defined as the sum of
the kinetic and (Born-Oppenheimer) potential energy, and minus the integrand
-
is the Hamiltonian of the system of nuclei, defined as the sum of
the kinetic and (Born-Oppenheimer) potential energy, and minus the integrand
-
![]() is usually called the mean force. The brackets denote an ensemble average
and the subscript indicates that the integrand is evaluated at the
point
is usually called the mean force. The brackets denote an ensemble average
and the subscript indicates that the integrand is evaluated at the
point
![]() along the reaction coordinate, where
along the reaction coordinate, where ![]() denotes the total of nuclear coordinates.
denotes the total of nuclear coordinates.
The S![]() 2 reaction studied in the present work is an activated process,
which implies that the barrier is too high for the reaction to take place
spontaneously within the time scale accessible to an MD simulation. The probability
to find the system close to the transition state is very small, and the reaction is
therefore a rare event. To nevertheless be able to estimate the mean force at the
reaction coordinate values of low probability, the method of constraint can be
used, where the dynamics of the system is performed with the reaction coordinate
fixed at a specified value
2 reaction studied in the present work is an activated process,
which implies that the barrier is too high for the reaction to take place
spontaneously within the time scale accessible to an MD simulation. The probability
to find the system close to the transition state is very small, and the reaction is
therefore a rare event. To nevertheless be able to estimate the mean force at the
reaction coordinate values of low probability, the method of constraint can be
used, where the dynamics of the system is performed with the reaction coordinate
fixed at a specified value ![]() .
The theoretical framework of the study of activated processes in an MD
simulation has been established some time ago in ref chandler78
and also ref CaCi89,
which provided a microscopic expression for the mean force. An
approximate version of this method [72,73], only
valid for reaction paths controlled by special classes of constraints,
has been successfully used in quite a number of simulations of
reactions.[74,75,54]
More recently, generally applicable expressions for the mean force
have been outlined [17,76],
which include the explicit terms to correct for the bias introduced in the ensemble
by applying the constraint (see also the appendix).
.
The theoretical framework of the study of activated processes in an MD
simulation has been established some time ago in ref chandler78
and also ref CaCi89,
which provided a microscopic expression for the mean force. An
approximate version of this method [72,73], only
valid for reaction paths controlled by special classes of constraints,
has been successfully used in quite a number of simulations of
reactions.[74,75,54]
More recently, generally applicable expressions for the mean force
have been outlined [17,76],
which include the explicit terms to correct for the bias introduced in the ensemble
by applying the constraint (see also the appendix).
|
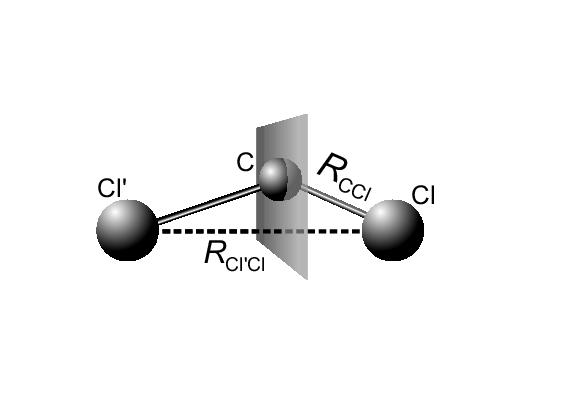
Here
![]() is the angle between the C-Cl
and Cl
is the angle between the C-Cl
and Cl![]() -Cl bonds.
In the following we will refer to Cl
-Cl bonds.
In the following we will refer to Cl![]() and Cl as the attacking
and leaving chloride, respectively. Since the reaction is symmetric,
the transition state is at a point where both C-Cl distances are
equal. At this transition state the value of the reaction coordinate
(equation 3.2) is
and Cl as the attacking
and leaving chloride, respectively. Since the reaction is symmetric,
the transition state is at a point where both C-Cl distances are
equal. At this transition state the value of the reaction coordinate
(equation 3.2) is ![]() , whereas it approaches zero for
separated reactants and one for separated products.
, whereas it approaches zero for
separated reactants and one for separated products.