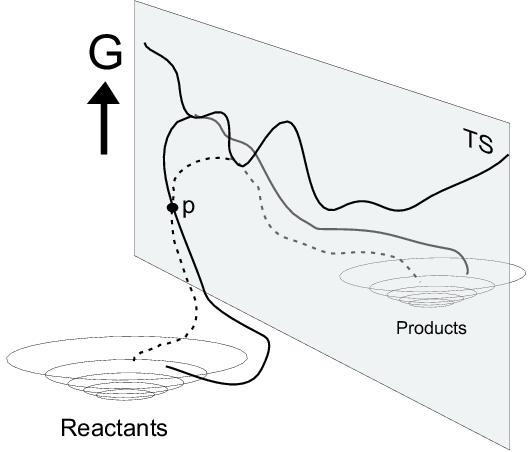
The technical details of transition path sampling and its potential to study the dynamics of rare events are described in a number of interesting papers by Bolhuis, Dellago, Geisler and Chandler[212,213,125]. The part that we are interested in, namely the generation and relaxation of reaction pathways, is schematically illustrated in figure 7.2.
|
In the rugged multidimensional free energy landscape,
we find two stable states: the reactant state and the product state,
which are separated from each other by an irregular energy barrier
depicted by the line in the plane in figure 7.2.
This line, in fact, connects all highest points of all the possible
(reaction) pathways from the reactant state to the product state.
We can define the transition path ensemble as the ensemble of all
possible trajectories connecting the two stable states, within a certain
finite time.
The two stable states can be regarded as basins of attraction so that
an MD simulation of the system started from a configuration in the
neighborhood of one of the stable states is very likely to sample only
this stable state region and will not be seen to cross the barrier to the
other stable state, unless we simulate for a very long time. Crossing the
barrier ridge is of course more probable through a low-lying pass than
via some high top on the ridge. However, if we manage to find a connecting
pathway over the barrier by some artificial manipulation of the system
(like we did for the hydrogen peroxide iron(II) complex, by first driving
out H
O from the coordination shell), we are likely to find a
too high barrier crossing point. Such an initial pathway is depicted in
figure 7.2 by the solid line from the reactant
state to the product state. If the found pathway is indeed not a
physically probable transition path, we can relax within the transition
path ensemble from the improbable pathway to more probable paths by
generating new pathways from our initial path.
We therefore randomly pick a point p on the initial pathway, from
where we branch off a new pathway, by making small random changes in
the atomic momenta. Integration of the
equations of motion forward and backward in time might result in
a new pathway (called a new generation), represented by the
dashed line. On this pathway,
we can again randomly pick a new point p and again generate a trial pathway,
etcetera. If the new trial pathway does not connect the two stable
states (within some arbitrarily chosen finite time span), but instead
remains in one of the stable states, we do not accept the new pathway
but repeat the procedure starting from another point on the previous pathway.
Success or failure of the pathway generation procedure depends on the
following points:
We want to make two more remarks on figure 7.2. First, it is possible that there exists more than one reaction ``channel'' separated from each other by an energy barrier. In figure 7.2, this is illustrated by the bump in the middle of the transition ridge, with lower lying passes on both sides (which even might lead to two different stable product states). Although in principle also pathways might be generated from the drawn pathway which pass through the right-hand-side channel, the chances of that become smaller as the separating bump increases. In practice another artificially initiated pathway would be needed as a starting point for the sampling of pathways through this second channel. The second remark regards the new definition of transition states within this theory. Instead of one transition state (TS) based on the intrinsic (zero Kelvin) reaction coordinate, an ensemble of transition states can be defined of all possible reaction pathways. The TS of each generated pathway is found by branching off a large number of new trajectories from a point p on the given pathway, starting with random momenta. From a point p close to one of the stable states most or even all trajectories will end up in the stable state. On the TS ridge however the chances are fifty-fifty to go either way, so that a point p from which half of the generated trajectories end up in each of the stable states can be identified as a point on the TS ridge. Of course, this TS point does not have to be connected to the highest potential energy along the pathway, since the TS is not only determined by the energy but also by the entropy. In particular, the potential energy along the pathway exhibits thermal fluctuation, which makes the maximum potential energy along the path a less useful parameter. We are e.g. not interested in the highest potential energy point if that high energy arises from motion (collision) of solvent molecules somewhere far from the reactants in the box. The TS point on a certain pathway should be a point on the free energy TS ridge. Having determined the TS points for a very large number (say, one thousand) of paths, interesting properties of the transition state ensemble (i.e. the ridge in figure 7.2) can be studied, such as the average solvent coordination in the transition state configurations.[125]
In the next section, we will first attempt to find the transition state for our initial pathway for the reaction between pentaaquairon(II) and hydrogen peroxide in water. Next we will use the transition path sampling technique to generate new pathways.